如图甲所示,光滑绝缘水平桌面上直立一个单匝正方形导线框ABCD,线框的边长为L=4 m、总电阻为R=1Ω.在直角坐标系xOy中,有界匀强磁场区域的下边界与x轴重合,上边界满足曲线方程y=2sin x(m),磁感应强度大小B=2 T.线框在沿x轴正方向的拉力F作用下,以速度v=1 m/s水平向右做匀速直线运动,直到拉出磁场.
x(m),磁感应强度大小B=2 T.线框在沿x轴正方向的拉力F作用下,以速度v=1 m/s水平向右做匀速直线运动,直到拉出磁场.
(1) 求线框中AD两端的最大电压;
(2) 在图乙中画出运动过程中线框i-t图象,并估算磁场区域的面积(估算结果保留2位有效数字);
(3) 求线框在穿越整个磁场的过程中,拉力F所做的功.
一列简谐横波沿AB方向由A质点传到B质点。已知A、B相距0.6m,横波的波长λ>0.5m。在某一时刻开始计时,质点A处于最大正位移处,经过0.1s,第二次回到平衡位置,此时质点B达到最大正位移处。请在图中画出0.1s时刻,质点A、B之间的波形图。并计算这列波的波速是多大?
如图甲所示的坐标系中,第四限象内存在垂直于纸面向里的有界匀强磁场,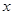 方向的宽度OA=20
方向的宽度OA=20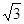 cm,
cm,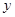 方向无限制,磁感应强度B0=1×10-4T。现有一比荷为q/m=2×1011C/kg的正离子以某一速度从O点射入磁场,α=60°,离子通过磁场后刚好从A点射出。
方向无限制,磁感应强度B0=1×10-4T。现有一比荷为q/m=2×1011C/kg的正离子以某一速度从O点射入磁场,α=60°,离子通过磁场后刚好从A点射出。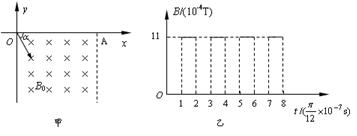
求离子进入磁场B0的速度的大小;
离子进入磁场B0后,某时刻再加一个同方向的匀强磁场,使离子做完整的圆周运动,求所加磁场磁感应强度的最小值;
离子进入磁场B0后,再加一个如图乙所示的变化磁场(正方向与B0方向相同,不考虑磁场变化所产生的电场),求离子从O点到A点的总时间。
如图所示,水平桌面处有水平向右的匀强电场,场强大小E=2´104V/m,A、B是完全相同的两个小物体,质量均为m=0.1kg,电量均为q=2´10-5C,且都带负电,原来都被按在桌面上的P点。现设法使A物体获得和电场E同方向的初速vA0=12m/s,A开始运动的加速度大小为6m/s2,经t时间后,设法使B物体获得和电场E同方向的初速vB0=6m/s(不计A、B两物体间的库仑力),求:
在A未与B相遇前,A电势能增量的最大值;
如果要使A尽快与B相遇,t为多大?
如图所示,有两本完全相同的书A、B,书重均为5 N,若将两本书等分成若干份后交叉地叠放在一起置于光滑桌面上,并将书A固定不动,用水平向右的力F把书B匀速抽出,现测得一组数据如下:
| 实验次数 |
1 |
2 |
3 |
4 |
… |
n |
| 将书分成的份数 |
2 |
4 |
8 |
16 |
… |
逐页交叉 |
| 力F的大小(N) |
4.5 |
10.5 |
22.5 |
46.5 |
… |
190.5 |
根据以上数据,试求:
若将书分成32份,力F应为多大?
该书的页数.
该书任意两张纸之间的动摩擦因数为多少?
随着机动车数量的增加,交通安全问题日益凸显。分析交通违法事例,将警示我们遵守交通法规,珍惜生命。一货车严重超载后的总质量为49t,以54km/h的速率匀速行驶。发现红灯时司机刹车,货车即做匀减速直线运动,加速度的大小为2.5m/s2(不超载时则为5m/s2)。若前方无阻挡,问从刹车到停下来此货车在超载及不超载时分别前进多远?
若超载货车刹车时正前方25m处停着总质量为1t的轿车,两车将发生碰撞,设相互作用0.1 s后获得相同速度,问货车对轿车的平均冲力多