如图,在某小区的休闲广场有一个正方形花园ABCD,为了便于观赏,要在AD、BC之间修一条小路,在AB、DC之间修另一条小路,使这两条小路等长.设计师给出了以下几种设计方案:
①如图1,E是AD上一点,过A作BE的垂线,交BE于点O,交CD于点H,则线段AH、BE为等长的小路;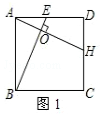
②如图2,E是AD上一点,过BE上一点O作BE的垂线,交AB于点G,交CD于点H,则线段GH、BE为等长的小路;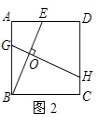
③如图3,过正方形ABCD内任意一点O作两条互相垂直的直线,分别交AD、BC于点E、F,交AB、CD于点G、H,则线段GH、EF为等长的小路;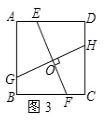
根据以上设计方案,解答下列问题:
(1)你认为以上三种设计方案都符合要求吗?
(2)要根据图1完成证明,需要证明△ ≌△ ,进而得到线段 = ;
(3)如图4,在正方形ABCD外面已经有一条夹在直线AD、BC之间长为EF的小路,想在直线AB、DC之间修一条和EF等长的小路,并且使这条小路的延长线过EF上的点O,请画草图(加以论述),并给出详细的证明.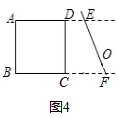
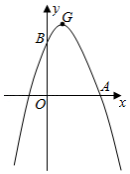
如图,抛物线 与 轴正半轴, 轴正半轴分别交于点 , ,且 ,点 为抛物线的顶点.
(1)求抛物线的解析式及点 的坐标;
(2)点 , 为抛物线上两点(点 在点 的左侧),且到对称轴的距离分别为3个单位长度和5个单位长度,点 为抛物线上点 , 之间(含点 , 的一个动点,求点 的纵坐标 的取值范围.
我们学习过利用尺规作图平分一个任意角,而“利用尺规作图三等分一个任意角”曾是数学史上一大难题,之后被数学家证明是不可能完成的.人们根据实际需要,发明了一种简易操作工具 三分角器.图1是它的示意图,其中 与半圆 的直径 在同一直线上,且 的长度与半圆的半径相等; 与 垂直于点 , 足够长.

使用方法如图2所示,若要把 三等分,只需适当放置三分角器,使 经过 的顶点 ,点 落在边 上,半圆 与另一边 恰好相切,切点为 ,则 , 就把 三等分了.
为了说明这一方法的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程.
已知:如图2,点 , , , 在同一直线上, ,垂足为点 , .
求证: .
暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.
方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用按八折优惠.
设某学生暑期健身 (次 ,按照方案一所需费用为 (元 ,且 ;按照方案二所需费用为 (元 ,且 .其函数图象如图所示.
(1)求 和 的值,并说明它们的实际意义;
(2)求打折前的每次健身费用和 的值;
(3)八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少?说明理由.

位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之一.
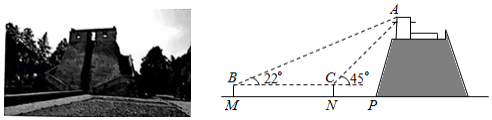
某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水平步道 上架设测角仪,先在点 处测得观星台最高点 的仰角为 ,然后沿 方向前进 到达点 处,测得点 的仰角为 .测角仪的高度为 .
(1)求观星台最高点 距离地面的高度(结果精确到 .参考数据: , , , ;
(2)“景点简介”显示,观星台的高度为 .请计算本次测量结果的误差,并提出一条减小误差的合理化建议.
为发展乡村经济,某村根据本地特色,创办了山药粉加工厂.该厂需购置一台分装机,计划从商家推荐试用的甲、乙两台不同品牌的分装机中选择.试用时,设定分装的标准质量为每袋 ,与之相差大于 为不合格.为检验分装效果,工厂对这两台机器分装的成品进行了抽样和分析,过程如下:
收集数据 从甲、乙两台机器分装的成品中各随机抽取20袋,测得实际质量(单位: 如下:
甲:501 497 498 502 513 489 506 490 505 486
502 503 498 497 491 500 505 502 504 505
乙:505 499 502 491 487 506 493 505 499 498
502 503 501 490 501 502 511 499 499 501
整理数据 整理以上数据,得到每袋质量 的频数分布表.
|
质量 频数 机器 |
|
|
|
|
|
|
|
甲 |
2 |
2 |
4 |
7 |
4 |
1 |
|
乙 |
1 |
3 |
5 |
7 |
3 |
1 |
分析数据 根据以上数据,得到以下统计量.
|
统计量 机器 |
平均数 |
中位数 |
方差 |
不合格率 |
|
甲 |
499.7 |
501.5 |
42.01 |
|
|
乙 |
499.7 |
|
31.81 |
|
根据以上信息,回答下列问题:
(1)表格中的 , ;
(2)综合上表中的统计量,判断工厂应选购哪一台分装机,并说明理由.