观察下面两个推理过程及结论:
若锐角 满足
满足 ,以角
,以角 分别为内角构造一个三角形,依据正弦定理和余弦定理可得到等式:
分别为内角构造一个三角形,依据正弦定理和余弦定理可得到等式: ,
,
若锐角 满足
满足 ,则
,则 ,以角
,以角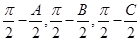 分别为内角构造一个三角形,依据正弦定理和余弦定理可以得到的等式:
分别为内角构造一个三角形,依据正弦定理和余弦定理可以得到的等式: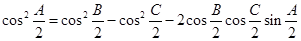 .
.
则:若锐角 满足
满足 ,类比上面推理方法,可以得到的一个等式是______________.
,类比上面推理方法,可以得到的一个等式是______________.
二项式(4x-2-x)6(x∈R)展开式中的常数项是________.
航空母舰“辽宁舰”将进行一次编队配置科学实验,要求2艘攻击型核潜艇一前一后,2艘驱逐舰和2艘护卫舰分列左、右,同侧不能都是同种舰艇,则舰艇分配方案的方法数为________.
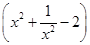 2的展开式中常数项是________.
2的展开式中常数项是________.
用1,2,3,4这四个数字组成无重复数字的四位数,其中恰有一个偶数字夹在两个奇数字之间的四位数的个数为________.
对于二次函数f(x)=ax2+bx+c,有下列命题:
①若f(p)=q,f(q)=p(p≠q),则f(p+q)=-(p+q);
②若f(p)=f(q)(p≠q),则f(p+q)=c;
③若f(p+q)=c(p≠q),则p+q=0或f(p)=f(q).
其中一定正确的命题是________(写出所有正确命题的序号).