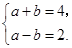如图,抛物线y=x2+bx+c过点A(﹣4,﹣3),与y轴交于点B,对称轴是x=﹣3,请解答下列问题:
(1)求抛物线的解析式.
(2)若和x轴平行的直线与抛物线交于C,D两点,点C在对称轴左侧,且CD=8,求△BCD的面积.
注:抛物线y=ax2+bx+c(a≠0)的对称轴是 .
.
解方程: (1)、  (2)、
(2)、 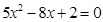
已知:在梯形ABCD中,CD∥AB,AD=DC=BC=2,AB=4.点M从A开始,以每秒1个单位的速度向点B运动;点N从点C出发,沿C→D→A方向,以每秒1个单位的速度向点A运动,若M、N同时出发,其中一点到达终点时,另一个点也停止运动.运动时间为t秒,过点N作NQ⊥CD交AC于点Q.
(1)设△AMQ的面积为S,求S与t的函数关系式,并写出t的取值范围.
(2)在梯形ABCD的对称轴上是否存在点P,使△PAD为直角三角形?若存在,求点P到AB的距离;若不存在,说明理由.
(3)在点M、N运动过程中,是否存在t值,使△AMQ为等腰三角形?若存在,求出t值;若不存在,说明理由.
我区某房地产开发公司于2013年5月份完工一商品房小区,6月初开始销售,其中6月的销售单价为0.7万元/m2,7月的销售单价为0.72万元/m2,且每月销售价格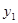 (单位:
(单位: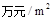 )与月份x(6≤x≤11,x为整数)之间满足一次函数关系,每月的销售面积为
)与月份x(6≤x≤11,x为整数)之间满足一次函数关系,每月的销售面积为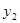 (单位:
(单位: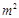 ),其中y2=-2000x+26000(6≤x≤11,x为整数).
),其中y2=-2000x+26000(6≤x≤11,x为整数).
(1)求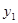 与月份
与月份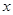 的函数关系式;
的函数关系式;
(2)6~11月中,哪一个月的销售额最高?最高销售额为多少万元?
(3)2013年11月时,因受某些因素影响,该公司销售部预计12月份的销售面积会在11月销售面积基础上减少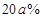 ,于是决定将12月份的销售价格在11月的基础上增加
,于是决定将12月份的销售价格在11月的基础上增加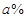 ,该计划顺利完成.为了尽快收回资金,2014年1月公司进行降价促销,该月销售额为(1500+600a)万元.这样12月、1月的销售额共为
,该计划顺利完成.为了尽快收回资金,2014年1月公司进行降价促销,该月销售额为(1500+600a)万元.这样12月、1月的销售额共为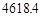 万元,请根据以上条件求出
万元,请根据以上条件求出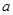 的值为多少?
的值为多少?
某校举办的课外活动中,有一项是小制作评比.作品上交时限为3月1日至30日,组委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1. 第三组的件数是12. 请你回答: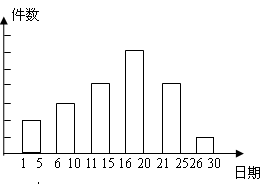
(1)本次活动共有__________件作品参赛;各组作品件数的中位数是_________件.
(2)经评比,第四组和第六组分别有10件和2件作品获奖,那么你认为这两组中哪个组获奖率较高?为什么?
(3)小制作评比结束后,组委会决定从4件最优秀的作品A、B、C、D中选出两件进行全校展示,请用树状图或列表法求出刚好展示B、D的概率.
先化简,再求值: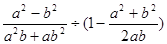 .其中
.其中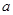 ,
,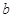 满足
满足