如图所示为某同学设计的节能运输系统．斜面轨道的倾角为37°，木箱与轨道之间的动摩擦因数μ＝0.25.设计要求：木箱在轨道顶端时，自动装货装置将质量m＝2.8kg的货物装入木箱，木箱载着货物沿轨道无初速滑下，当轻弹簧被压缩至最短时，自动装货装置立刻将货物卸下，然后木箱恰好被弹回到轨道顶端，接着再重复上述过程．若g取10 m/s2，sin37°＝0.6 ，cos37°＝0.8.求：满足设计要求的木箱质量．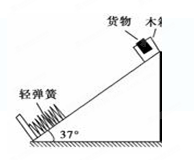
如图所示，将一根光滑的细金属棒折成“V”形，顶角为2θ，其对称轴竖直，在其中一边套一个质量为m的小金属环P。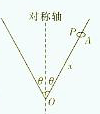
若固定“V”形细金属棒，小金属环P从距离顶点O为x的A点处由静止自由滑下，则小金属环由静止下滑至顶点O需多长时间？
若小金属环P随“V”形细金属棒绕其对称轴以每秒n转匀速转动时，则小金属环离对称轴的距离为多少？
如图所示的匀强电场中，有a、b、c三点，ab=5cm，bc=12cm，其中ab沿电场方向，bc和电场方向成600角，一个电荷量为q=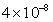
C的正电荷从a移到b电场力做功为Wl=
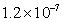J，求：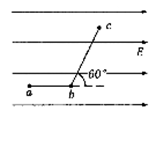
匀强电场的场强E
电荷从b移到c，电场力做功W2
a、c两点的电势差
如图所示，水平放置的平行板电容器极板间距离为d，加的电压为U0，上极板带正电。现有一束微粒以某一速度垂直于电场方向沿中心线OO′射入，并能沿水平方向飞出电场。求：
带何种电荷？
带电微粒的比荷（q/m）是多少？
如图所示，在光滑绝缘的水平轨道上方同时存在着水平向右的匀强电场和垂直纸面向里的匀强磁场，磁场的磁感应强度B＝0.1T。一质量m=1.0×10-2kg、带电量q＝+1.0×10-2C可视为质点的物块，从轨道上的M点无初速度释放，当该物块沿直线运动到达轨道上的N点时，恰好对轨道无压力，求此时速度多大？（g＝10m/s2）
如图所示的区域中，左边为垂直纸面向里的匀强磁场，磁感应强度为 B ，右边是一个电场强度大小未知的匀强电场，其方向平行于OC且垂直于磁场方向．一个质量为m 、电荷量为-q 的带电粒子从P孔以初速度V0沿垂直于磁场方向进人匀强磁场中，初速度方向与边界线的夹角θ＝600，粒子恰好从C孔垂直于OC射入匀强电场，最后打在Q点，已知OQ＝ 2 OC ，不计粒子的重力，求：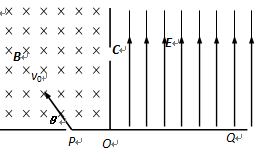
粒子从P运动到Q所用的时间 t 。
电场强度 E 的大小
粒子到达Q点时的动能EkQ