如图,抛物线y=a(x﹣h)2+k经过点A(0,1),且顶点坐标为B(1,2),它的对称轴与x轴交于点C.
(1)求此抛物线的解析式.
(2)在第一象限内的抛物线上求点P,使得△ACP是以AC为底的等腰三角形,请求出此时点P的坐标.
(3)上述点是否是第一象限内此抛物线上与AC距离最远的点?若是,请说明理由;若不是,请求出第一象限内此抛物线上与AC距离最远的点的坐标.
(1)如图,在矩形ABCD中,BF=CE,求证:AE=DF;
(2)如图,在圆内接四边形ABCD中,O为圆心,∠BOD=160°,求∠BCD的度数.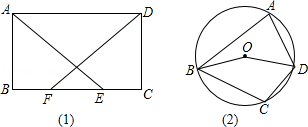
(1)化简:(x+2)2+x(x+3)
(2)解不等式组: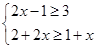 .
.
如图,直线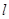 ⊥线段
⊥线段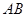 于点
于点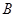 ,点
,点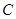 在
在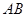 上,且
上,且 ,点
,点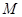 是直线
是直线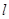 上的动点,作点
上的动点,作点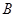 关于直线
关于直线 的对称点
的对称点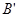 ,直线
,直线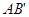 与直线
与直线 相交于点
相交于点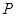 ,连接
,连接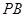
(1)如图1,若点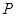 与点
与点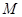 重合,则∠
重合,则∠ =°,线段
=°,线段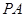 与
与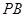 的比值为;
的比值为;
(2)如图2,若点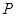 与点
与点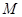 不重合,设过
不重合,设过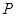 、
、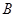 、
、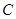 三点的圆与直线
三点的圆与直线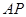 相交于
相交于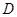 ,连接
,连接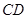 。求证:①
。求证:①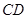 =
=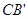 ;②
;②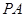 =2
=2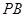 ;
;
(3)如图3,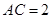 ,
,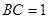 ,则满足条件
,则满足条件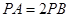 的点都在一个确定的圆上,在以下两小题中选做一题:
的点都在一个确定的圆上,在以下两小题中选做一题:
①如果你能发现这个确定圆的圆心和半径,那么不必写出发现过程,只要证明这个圆上的任意一点Q,都满足QA=2QB
②如果你不能发现这个确定圆的圆心和半径,那么请取几个特殊位置的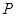 点,如点
点,如点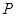 在直线
在直线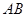 上、点
上、点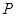 与点
与点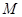 重合等进行探究,求这个圆的半径
重合等进行探究,求这个圆的半径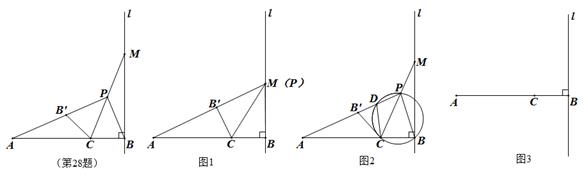
科研所计划建一幢宿舍楼,因为科研所实验中会产生辐射,所以需要有两项配套工程:①在科研所到宿舍楼之间修一条笔直的道路;②对宿舍楼进行防辐射处理,已知防辐射费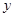 万元与科研所到宿舍楼的距离
万元与科研所到宿舍楼的距离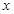
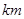 之间的关系式为:
之间的关系式为: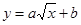 (0≤
(0≤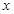 ≤9),当科研所到宿舍楼的距离为1
≤9),当科研所到宿舍楼的距离为1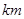 时,防辐射费用为720万元;当科研所到宿舍楼的距离为9
时,防辐射费用为720万元;当科研所到宿舍楼的距离为9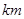 或大于9
或大于9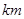 时,辐射影响忽略不计,不进行防辐射处理,设每公里修路的费用为
时,辐射影响忽略不计,不进行防辐射处理,设每公里修路的费用为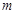 万元,配套工程费
万元,配套工程费 =防辐射费+修路费
=防辐射费+修路费
(1)当科研所到宿舍楼的距离为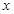 =9
=9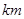 时,防辐射费
时,防辐射费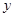 =万元;
=万元;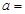 ,
,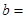
(2)若每公里修路的费用为90万元,求当科研所到宿舍楼的距离为多少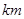 时,配套工程费最少?
时,配套工程费最少?
(3)如果配套工程费不超过675万元,且科研所到宿舍楼的距离小于9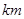 ,求每公里修路费用
,求每公里修路费用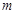 万元的最大值
万元的最大值
平面直角坐标系中,点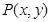 的横坐标
的横坐标 的绝对值表示为
的绝对值表示为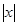 ,纵[坐标
,纵[坐标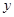 的绝对值表示为
的绝对值表示为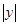 ,我们把点
,我们把点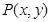 的横坐标与纵坐标的绝对值之和叫做点
的横坐标与纵坐标的绝对值之和叫做点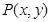 的勾股值,记为:「
的勾股值,记为:「 」,即「
」,即「 」=
」=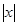 +
+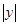 ,(其中的“+”是四则运算中的加法)
,(其中的“+”是四则运算中的加法)
(1)求点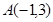 ,
,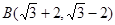 的勾股值「
的勾股值「 」、「
」、「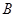 」
」
(2)点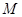 在反比例函数
在反比例函数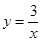 的图像上,且「
的图像上,且「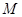 」=4,求点
」=4,求点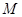 的坐标;
的坐标;
(3)求满足条件「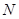 」=3的所有点
」=3的所有点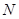 围成的图形的面积
围成的图形的面积