已知二次函数y=ax2+bx+c(a≠0)的图象经过点(1,0),(5,0),(3,﹣4).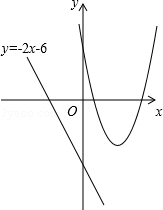
(1)求该二次函数的解析式;
(2)当y>﹣3,写出x的取值范围;
(3)A、B为直线y=﹣2x﹣6上两动点,且距离为2,点C为二次函数图象上的动点,当点C运动到何处时△ABC的面积最小?求出此时点C的坐标及△ABC面积的最小值.
某农场的一个开发商准备开发建设甲、乙两种户型的楼房,甲种楼房每套造价12万元,售价14.5万元;乙种楼房每套造价8万元,售价10万元,且它们的造价和售价始终不变.现准备建造甲、乙两种楼房共20套,所用资金不低于190万元,不高于200万元.
(1)该开发商有哪几种建造方案?
(2)该开发商采用哪种建造方案可获得最大利润?最大利润是多少?
(3)若用(2)中所求得的利润再次建造楼房,请直接写出获得最大利润的建造方案.
我县化工园区一化工厂,组织20辆汽车装运A、B、C三种化学物资共200吨到某地.按计划20辆汽车都要装运,每辆汽车只能装运同一种物资且必须装满.请结合表中提供的信息,
| 物资种类 |
A |
B |
C |
| 每辆汽车运载量(吨) |
12 |
10 |
8 |
| 每吨所需运费(元/吨) |
240 |
320 |
200 |
解答下列问题:
(1)设装运A种物资的车辆数为x,装运B种物资的车辆数为y.求y与x的函数关系式;
(2)如果装运A种物资的车辆数不少于5辆,装运B种物资的车辆数不少于4辆,若要求总运费最少,应如何安排使得总运费最少,并求出最少总运费.
冷饮店每天需配制甲、乙两种饮料共50瓶,已知甲饮料每瓶需糖14克,柠檬酸5克;乙种饮料每瓶需糖6克,柠檬酸10克。现有糖500克,柠檬酸400克.
(1)请计算有几种配制方案能满足冷饮店的要求?
(2)冷饮店对两种饮料上月的销售情况作了统计,结果如下表。请你根据这些统计数据确定一种比较合理的配制方案,并说明理由.
| 两种饮料 的日销量 |
甲 |
10 |
12 |
14 |
16 |
21 |
25 |
30 |
38 |
40 |
50 |
| 乙 |
40 |
38 |
36 |
34 |
29 |
25 |
25 |
12 |
10 |
0 |
|
| 天数 |
3 |
4 |
4 |
4 |
8 |
1 |
1 |
1 |
2 |
2 |
|
荣昌公司要将本公司100吨货物运往某地销售,经与春晨运输公司协商,计划租用甲、乙两种型号的汽车共6辆,用这6辆汽车一次将货物全部运走,其中每辆甲型汽车最多能装该种货物16吨,每辆乙型汽车最多能装该种货物18吨.已知租用1辆甲型汽车和2辆乙型汽车共需费用2500元;租用2辆甲型汽车和1辆乙型汽车共需费用2450元,
且同一型号汽车每辆租车费用相同.
(1)求租用一辆甲型汽车、一辆乙型汽车的费用分别是多少元?
(2)若荣昌公司计划此次租车费用不超过5000元,通过计算求出该公司有几种租车方案?请你设计出来,并求出最低的租车费用.
菜农李伟种植的某蔬菜计划以每千克5元的单价对外批发销售,由于部分菜农盲目扩大种植,造成该蔬菜滞销.李伟为了加快销售,减少损失,对价格经过两次下调后,以每千克3.2元的单价对外批发销售.
(1)求平均每次下调的百分率;
(2)小华准备到李伟处购买5吨该蔬菜,因数量多,李伟决定再给予两种优惠方案以供选择:
方案一:打九折销售;
方案二:不打折,每吨优惠现金200元.
试问小华选择哪种方案更优惠,请说明理由.