已知抛物线的顶点为(0,4)且与x轴交于(﹣2,0),(2,0).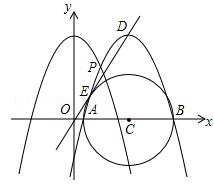
(1)直接写出抛物线解析式;
(2)如图,将抛物线向右平移k个单位,设平移后抛物线的顶点为D,与x轴的交点为A、B,与原抛物线的交点为P.
①当直线OD与以AB为直径的圆相切于E时,求此时k的值;
②是否存在这样的k值,使得点O、P、D三点恰好在同一条直线上?若存在,求出k值;若不存在,请说明理由.
图①、图②均为4×4的正方形网格,线段AB、BC的端点均在网点上.按要求在图①、图②中以AB和BC为边各画一个四边形ABCD.
要求:四边形ABCD的顶点D在格点上,且有两个角相等(一组或两组角相等均可);所画的两个四边形不全等.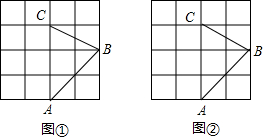
如图,有一个晾衣架放置在水平地面上,在其示意图中,支架OA、OB的长均为108cm,支架OA与水平晾衣杆OC的夹角∠AOC为59°,求支架两个着地点之间的距离AB.(结果精确到0.1cm)(参考数据:sin59°=0.86,cos59°=0.52,tan59°=1.66).
长春市某校准备组织七年级学生游园,供学生选择的游园地点有:东北虎园、净月潭、长影世纪城,每名学生只能选择其中一个地点.该校学生会从七年级学生中随机抽取了a名学生,对他们选择各游园点的情况进行了调查,并根据调查结果绘制成如下条形统计图.
(1)求a的值.
(2)求这a名学生选择去净月潭游园的人数的百分比.
(3)按上述调查结果,估计该校七年级650名学生中选择去净月潭游园的人数.
如图,在同一平面内,有一组平行线l1、l2、l3,相邻两条平行线之间的距离均为4,点O在直线l1上,⊙O与直线l3的交点为A、B,AB=12,求⊙O的半径.
某班有45名同学参加紧急疏散演练.对比发现:经专家指导后,平均每秒撤离的人数是指导前的3倍,这45名同学全部撤离的时间比指导前快3秒.求指导前平均每秒撤离的人数.