1897年汤姆孙发现电子后,许多科学家为测量电子的电荷量做了大量的探索。1907~1916年密立根用带电油滴进行实验,发现油滴所带的电荷量是某一数值e的整数倍,于是称这数值e为基本电荷。
如图所示,完全相同的两块金属板正对着水平放置,板间距离为d。当质量为m的微小带电油滴在两板间运动时,所受空气阻力的大小与速度大小成正比。两板间不加电压时,可以观察到油滴竖直向下做匀速运动,通过某一段距离所用时间为t1;当两板间加电压U(上极板的电势高)时,可以观察到同一油滴竖直向上做匀速运动,且在时间t2内运动的距离与在时间t1内运动的距离相等。忽略空气浮力,重力加速度为g。
(1)判断上述油滴的电性,要求说明理由;
(2)求上述油滴所带的电荷量Q;
(3)在极板间照射X射线可以改变油滴的带电量。再采用上述方法测量油滴的电荷量。如此重复操作,测量出油滴的电荷量Qi,如下表所示。如果存在基本电荷,那么油滴所带的电荷量Qj应为某一最小单位的整数倍,油滴电荷量的最大公约数(或油滴带电量之差的最大公约数)即为基本电荷e。请根据现有数据求出基本电荷的电荷量e (保留3位有效数字)。
| 实验次序 |
1 |
2 |
3 |
4 |
5 |
| 电荷量Qi(10-18C) |
0.95 |
1.10 |
1.41 |
1.57 |
2.02 |
如图,光滑水平面AB与竖直面的半圆形导轨在B点相连接,导轨半径为R,一质量为m的静止木块在A处压缩弹簧,释放后,木块获得一向右的初速度,当它经过B点进入导轨瞬间对导轨的压力是其重力的7倍,之后向上运动恰能通过轨道顶点C,不计空气阻力,试求:
(1)弹簧对木块所做的功;
(2)木块从B到C过程中克服摩擦力做的功;
(3)木块离开C点落回水平面所需的时间和落回水平面时的动能。
某人用100N的力将一质量为50g的小球以10m/s的速度从某一高处竖下向下抛出,经1s小球刚好落地,不考虑空气阻力,选地面为零势能点,g=10m/s2。求:
(1)小球刚抛出时的动能和势能各多大?
(2)小球着地时的动能和势能各多大?
汽车发动机的额定功率为30KW,质量为2000kg,当汽车在水平路面上行驶时受到阻力为车重的0.1倍,
(1)汽车在路面上能达到的最大速度?
(2)当汽车速度为10m/s时的加速度?
如图所示,质量均为m的小车和木箱紧挨着静止在光滑的水平冰面上,质量为2m的小孩站在小车上用力向右迅速推出木箱,木箱相对于冰面运动的速度为v,木箱运动到右侧墙壁时与竖直墙壁发生弹性碰撞,反弹后能被小孩接住,求: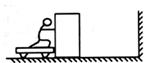
①小孩接住箱子后共同速度的大小.
②若小孩接住箱子后再次以相对于冰面的速度v将木箱向右推出,木箱仍与竖直墙壁发生弹性碰撞,判断小孩能否再次接住木箱.
(8分)如图所示,是一透明半圆柱体的横截面,O为横截面的圆心,其半径为R,折射率为,OA水平且垂直截面, 从A点射出一条光线AB经折射后水平射出半圆柱体,已知OA=R,光速为c.求: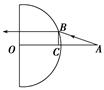
(ⅰ)光在透明半圆柱体中的传播速度;
(ⅱ)入射点B到OA的垂直距离BC。