如图,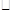 ABCD中,AB=2,以点A为圆心,AB为半径的圆交边BC于点E,连接DE、AC、AE.
ABCD中,AB=2,以点A为圆心,AB为半径的圆交边BC于点E,连接DE、AC、AE.
(1)求证:△AED≌△DCA;
(2)若DE平分∠ADC且与⊙A相切于点E,求图中阴影部分(扇形)的面积.
计算: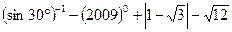
如图,直线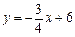 分别与x轴、y轴交于A、B两点;直线
分别与x轴、y轴交于A、B两点;直线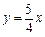 与AB交于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿x轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位
与AB交于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿x轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位 ),点E的运动时间为t(秒).
),点E的运动时间为t(秒).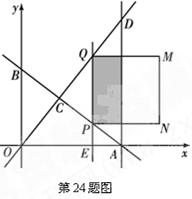
⑴求点C的坐标.
⑵当0<t<5时,求S与t之间的函数关系式.
⑶求⑵中S的最大值.
⑷当t>0时,直接写出点(4, )在正方形PQMN内部时t的取值范围.
)在正方形PQMN内部时t的取值范围.
已知一次函数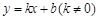 和反比例函数
和反比例函数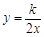 的图象交于点A(1,1).
的图象交于点A(1,1).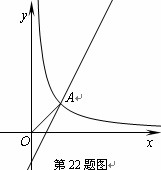
⑴求两个函数的解析式;
⑵若点B是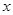 轴上一点,且△AOB是直角三角形,求B点的坐标.
轴上一点,且△AOB是直角三角形,求B点的坐标.
如图是某人在方格纸中设计图案的一部分,请你帮他完成余下的工作:

(1)作出关于直线AB对称的图形;
(2)将你画出的部分连同原图形绕点O逆时针旋转90°.
(两道小题分别在下面两图中完成,不用写作法)
(本小题满分10分)
北京奥运会开幕前,某体育用品商场预测某品牌运动服能够畅销,就用32 000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元
000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元 .
.
⑴该商场两次共购进这种运动服多少套?
⑵如果这两批运动服每套的售价相同,且全部售完后总利润率不低于20%,那么每套售价至少是多少元?(利润率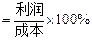 )
)