我们知道,三角形的三条中线一定会交于一点,这一点就叫做三角形的重心.重心有很多美妙的性质,如关于线段比.面积比就有一些“漂亮”结论,利用这些性质可以解决三角形中的若干问题.请你利用重心的概念完成如下问题: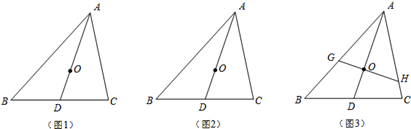
(1)若O是△ABC的重心(如图1),连结AO并延长交BC于D,证明: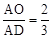 ;
;
(2)若AD是△ABC的一条中线(如图2),O是AD上一点,且满足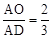 ,试判断O是△ABC的重心吗?如果是,请证明;如果不是,请说明理由;
,试判断O是△ABC的重心吗?如果是,请证明;如果不是,请说明理由;
(3)若O是△ABC的重心,过O的一条直线分别与AB、AC相交于G、H(均不与△ABC的顶点重合)(如图3),S四边形BCHG,S△AGH分别表示四边形BCHG和△AGH的面积,试探究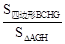 的最大值.
的最大值.
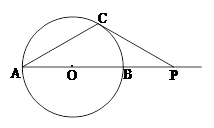
如图,⊙O的直径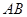 =6cm,
=6cm,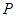 是
是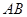 延长线上的一点,过
延长线上的一点,过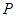 点作⊙O的切线,切点为
点作⊙O的切线,切点为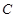 ,连接
,连接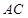 .
.
(1)若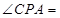 30°,求PC的长;
30°,求PC的长;
(2)若点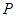 在
在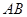 的延长线上运动,
的延长线上运动,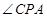 的平分线交
的平分线交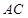 于点
于点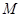 ,你认为∠
,你认为∠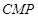 的大小是否发生变化?若变化,请说明理由;若不变,求出∠
的大小是否发生变化?若变化,请说明理由;若不变,求出∠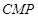 的值.
的值.
某校七(1)班同学分三组进行数学活动,对七年级400名同学最喜欢喝的饮料情况、八年级300名同学零花钱的最主要用途情况、九年级300名同学完成家庭作业时间情况进行了全面调查,并分别用扇形图、频数分布直方图、表格来描述整理得到的数据.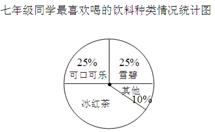
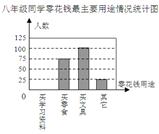
九年级同学完成家庭作业时间情况统计表
| 时间 |
1小时左右 |
1.5小时左右 |
2小时左右 |
2.5小时左右 |
| 人数 |
50 |
80 |
120 |
50 |
根据以上信息,请回答下列问题:
(1)七年级400名同学中最喜欢喝“冰红茶”的人数是多少?
(2)补全八年级300名同学中零花钱的最主要用途情况频数分布直方图;
(3)九年级300名同学中完成家庭作业的平均时间大约是多少小时(结果保留一位小数)?
小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了60次实验,实验的结果如下:
| 朝上的点数 |
1 |
2 |
3 |
4 |
5 |
6 |
| 出现的次数 |
7 |
9 |
6 |
8 |
20 |
10 |
(1)计算“3点朝上”的频率和“5点朝上”的频率.
(2)小颖说:“根据实验,一次实验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次.”小颖和小红的说法正确吗?为什么?
(3)小颖和小红各投掷一枚骰子,用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率.
工人师傅要将一块如图(1)所示的白铁皮,经过适当的剪切后,焊接成一块与白铁皮面积相等的正方形铁皮(焊接时不计材料的损耗),按要求完成下列各题:


(1)正方形的边长为;
(2)请在图(1)中用虚线画出剪切线;
(3)在图(2)的方格纸中画出图(1)剪切后所拼成正方形的图案(保留拼接痕迹,不写画法).
计算:(1) .
.
(2)解不等式: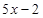 >
>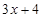 .
.