某校九年级有1200名学生,在体育考试前随机抽取部分学生进行体能测试,成绩分别记为A、B、C、D共四个等级,其中A级和B级成绩为“优”,将测试结果绘制成如下条形统计图和扇形统计图.

(1)求抽取参加体能测试的学生人数;
(2)估计该校九年级全体学生参加体能测试成绩为“优”的学生共有多少人?
如图,已知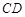 是⊙
是⊙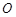 的直径,弦
的直径,弦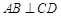 ,垂足为点
,垂足为点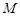 ,点
,点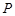 是
是 上一点,且
上一点,且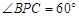 .
.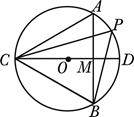
试判断 的形状,并说明你的理由.
的形状,并说明你的理由.
某校决定对初三学生进行体育成绩测试,成绩记入总分,同学们将根据自己平时的运动成绩确定自己的参考项目,下面是小亮同学的两个项目立定跳远和一分钟跳绳在近期连续五次测试的得分情况(立定跳远得分统计表和一分钟跳绳得分折线图):
立定跳远得分统计表
| 测试 日期 |
星期一 |
星期二 |
星期三 |
星期四 |
星期五 |
| 得分 |
7 |
10 |
8 |
9 |
6 |

(1)请根据以上信息,分别将这两个项目的平均数、极差、方差填入下表:
| 统计量 |
平均数 |
极差 |
方差 |
| 立定跳远 |
8 |
||
| 一分钟跳绳 |
2 |
0.4 |
(2)根据以上信息,你认为在立定跳远和一分钟跳绳这两个项目中,小亮应选择哪个项目作为体育考试的参考项目?请简述理由.
解方程: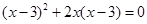
计算: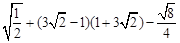
某楼盘一楼是车库(暂不销售),二楼至二十三楼均为商品房(对外销售).商品房售价方案如下:第八层售价为3000元/米2,从第八层起每上升一层,每平方米的售价增加40元;反之,楼层每下降一层,每平方米的售价减少20元.已知商品房每套面积均为120平方米.开发商为购买者制定了两种购房方案:
方案一:购买者先交纳首付金额(商品房总价的30%),再办理分期付款(即贷款).
方案二:购买者若一次付清所有房款,则享受8%的优惠,并免收五年物业管理费(已知每月物业管理费为a元)
(1)请写出每平方米售价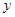 (元/米2)与楼层
(元/米2)与楼层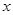 (2≤
(2≤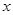 ≤23,
≤23,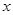 是正整数)之
是正整数)之
间的函数解析式;
(2)小张已筹到120000元,若用方案一购房,他可以购买哪些楼层的商品房呢?
(3)有人建议老王使用方案二购买第十六层,但他认为此方案还不如不免收物业管理费而直接享受9%的优惠划算.你认为老王的说法一定正确吗?请用具体的数据阐明你的看法.