在一个边长为a（单位：cm）的正方形ABCD中，点E、M分别是线段AC，CD上的动点，连结DE并延长交正方形的边于点F，过点M作MN⊥DF于H，交AD于N．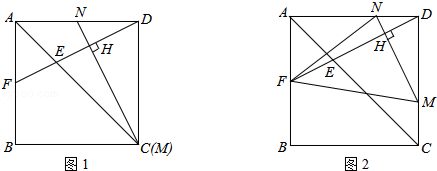
（1）如图1，当点M与点C重合，求证：DF=MN；
（2）如图2，假设点M从点C出发，以1cm/s的速度沿CD向点D运动，点E同时从点A出发，以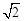
cm/s速度沿AC向点C运动，运动时间为t（t＞0）；
①判断命题“当点F是边AB中点时，则点M是边CD的三等分点”的真假，并说明理由．
②连结FM、FN，△MNF能否为等腰三角形？若能，请写出a，t之间的关系；若不能，请说明理由．
x-1=0；