若正数项数列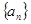 的前
的前 项和为
项和为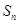 ,首项
,首项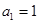 ,点
,点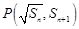 在曲线
在曲线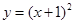 上.
上.
(1)求 ;
;
(2)求数列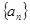 的通项公式
的通项公式 ;
;
(3)设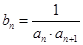 ,
, 表示数列
表示数列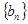 的前项和,若
的前项和,若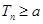 恒成立,求
恒成立,求 及实数
及实数 的取值范围.
的取值范围.
复数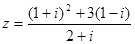 ,若
,若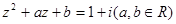 ,求
,求 的值.
的值.
【原创】已知函数 满足以下条件:①定义在正实数集上;②
满足以下条件:①定义在正实数集上;② ;③对任意实数
;③对任意实数 ,都有
,都有 。
。
(1)求 ,
, 的值;
的值;
(2)求证:对于任意 ,都有
,都有 ;
;
(3)若不等式 ,对
,对 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
已知函数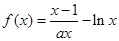 (
(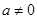 )
)
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)当 时,求
时,求 在
在 上的最大值和最小值(
上的最大值和最小值( );
);
(Ⅲ)求证: .
.
将编号为1、2、3、4的四个小球放入甲、乙、丙三只盒子内.
(1)若三只盒子都不空,且3号球必须在乙盒内有多少种不同的放法;
(2)若1号球不在甲盒内,2号球不在乙盒内,有多少种不同放法。(均须先列式再用数字作答)
观察下列各不等式: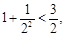
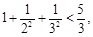
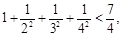
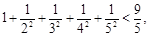
…
(1)由上述不等式,归纳出一个与正整数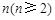 有关的一般性结论;
有关的一般性结论;
(2)用数学归纳法证明你得到的结论.