如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).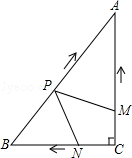
(1)当t为何值时,以A,P,M为顶点的三角形与△ABC相似?
(2)是否存在某一时刻t,使四边形APNC的面积S有最小值?若存在,求S的最小值;若不存在,请说明理由.
(本小题满分6分)已知:如图, ,
, 是□ABCD的对角线
是□ABCD的对角线 上的两点,
上的两点,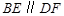 ,求证:
,求证: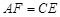 .
.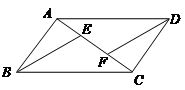
(1)AB∥CD,如图1,点P在AB、CD外面时,由AB∥CD,有∠B=∠BOD,又因为∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B-∠D.如图2,将点P移到AB、CD内部,以上结论是否成立?若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论.
(2)如图3,若AB、CD相交于点Q,则∠BPD、∠B、∠D、∠BQD之间有何数量关系(不需证明)?
(3)根据(2)的结论求图4中∠A+∠B+∠C+∠D+∠E+∠F的度数.
(4)若平面内有点A1、A2、A3、A4、A5、A6、A7、A8,连结A1A3、A2A4、A3A5、A4A6、A5A7、A6A8、A7 A1、A8 A2,如图5,则∠A1+∠A2+∠A3+∠A4+∠A5+∠A6+∠A7+∠A8的度数是多少(直接写出结果)?
若平面内有n个点A1、A2、A3、A4、A5、······,An,且这n个点能围成的多边形为凸多边形,连结A1A3、A2A4、A3A5、A4A6、A5A7,······,An-1A1、AnA2,则∠A1+∠A2+∠A3+∠A4+······+∠An-1+∠An的度数是多少(直接写出结果,用含n的代数式表示)?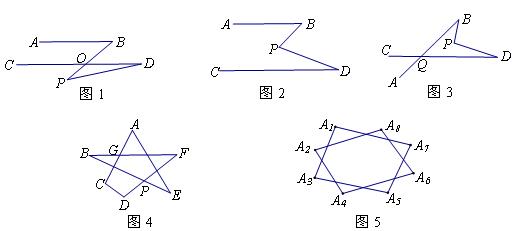
对x,y定义一种新运算T,规定:T(x,y)=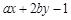 (其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=
(其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=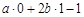 =2b-1.
=2b-1.
(1)已知T(1,﹣1)=﹣2,T(4,2)=3.
①求a,b的值;
②若关于m的不等式组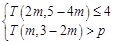 恰好有2个整数解,求实数p的取值范围;
恰好有2个整数解,求实数p的取值范围;
(2)若T(x,y)=T(y,x)对任意实数x,y都成立(这里T(x,y)和T(y,x)均有意义),则a,b应满足怎样的关系式?
某服装店用10000元购进A,B两种新式服装,按标价售出后可获得毛利润5400元(毛利润=售价﹣进价),这两种服装的进价、标价如表所示:
| 类型、价格 |
A型 |
B型 |
| 进价(元/件) |
80 |
100 |
| 标价(元/件) |
120 |
160 |
(1)这两种服装各购进的件数;
(2)如果A种服装按标价的8折出售,要使这批服装全部售出后毛利润不低于2000元,则B种服装至多按标价的几折出售?
如图,方格中有一条美丽可爱的小金鱼.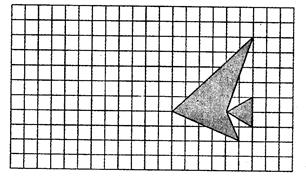
(1)若方格的边长为1,则小鱼的面积为.
(2)画出小鱼向左平移10格后的图形(不要求写作图步骤和过程).