一个不透明的口袋里装有分别标有汉字“灵”、“秀”、“鄂”、“州”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,球上的汉字刚好是“鄂”的概率为多少?
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图的方法,求出甲取出的两个球上的汉字恰能组成“灵秀”或“鄂州”的概率P1;
(3)乙从中任取一球,记下汉字后再放回袋中,然后再从中任取一球,记乙取出的两个球上的汉字恰能组成“灵秀”或“鄂州”的概率为P2,指出P1,P2的大小关系(请直接写出结论,不必证明).
、萧山新星塑料厂有甲、乙、丙三辆运货车,每辆车只负责进货或出货,丙车每小时的运输量最多,乙车每小时的运输量最少,乙车每小时运6吨,下图是甲、乙、丙三辆运输车开始工作后,仓库的库存量y(吨)与工作时间x(小时)之间的函数图像,其中OA段只有甲、丙两车参与运输,AB段只有乙、丙两车参与运输,BC段只有甲、乙两车参与运输。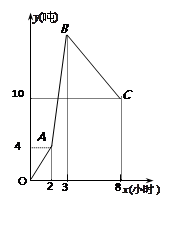
(1)甲、乙、丙三辆车中,谁是进货车?
(2)甲车和丙车每小时各运输多少吨?
(3)由于仓库接到临时通知,要求三车在8小时后同时开始工作,但丙车在运送
10吨货物后出现故障而退出,问:8小时后,甲、乙两车又工作了几小时,使仓库的库存量为6吨?
新年新举措——我县某工艺品销售公司今年一月份调整了职工的月工资分配方案,调整后月
工资由基本保障工资和计件奖励工资两部分组成(计件奖励工资=销售每件的奖励金额×销
售的件数). 下表是甲、乙两位职工今年2月份的工资情况信息:
| 职工 |
甲 |
乙 |
| 月销售件数(件) |
200 |
300 |
| 月工资(元) |
2000 |
2500 |
(1)试求工资分配方案调整后职工的月基本保障
工资和销售每件产品的奖励金额各是多少?
(2)若职工丙今年三月份的工资不低于3000元,
那么丙该月至少应销售多少件产品?
某学校组织九年级学生参加社会实践活动,若单独租用35座客车若干辆,则刚好坐满;若单独租用55座客车,则可以少租一辆,且余45个空座位,求该校九年级学生参加社会实践活动的人数.
列方程(组)解应用题
国家的“家电下乡”政策激活了农民购买能力,提高了农民的生活水平。“家电下乡”的补贴标准是:农户每购买一件家电,国家将按每件家电售价的13%补贴给农户.李大叔购买了一台彩电和一台洗衣机,从乡政府领到了390元补贴款. 若彩电的售价比洗衣机的售价高1000元,求彩电和洗衣机的售价各是多少元.
解方程组:
10.某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:(注:获利=售价-进价),若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?
| 甲 |
乙 |
|
| 进价(元/件) |
15 |
35 |
| 售价(元/件) |
20 |
45 |