如图，在平面直角坐标系中，有一条直线l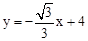：与x轴、y轴分别交于-优题课

如图，在平面直角坐标系中，有一条直线l：与x轴、y轴分别交于点M、N，一个高为3的等边三角形ABC，边BC在x轴上，将此三角形沿着x轴的正方向平移．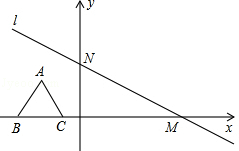

（1）在平移过程中，得到△A₁B₁C₁，此时顶点A₁恰落在直线l上，写出A₁点的坐标　　；
（2）继续向右平移，得到△A₂B₂C₂，此时它的外心P恰好落在直线l上，求P点的坐标；
（3）在直线l上是否存在这样的点，与（2）中的A₂、B₂、C₂任意两点能同时构成三个等腰三角形？如果存在，求出点的坐标；如果不存在，说明理由．

科目数学题型解答题难度较难

知识点：坐标与图形变化-旋转

（1）计算： ${(π - 2019)}^{0} + | \sqrt{2} - 1 | + 2 \cos 45 °$ ；

（2）计算： $(1 + \frac{1}{x - 1}) \div \frac{x}{x^{2} - 1}$ ．

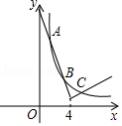
如图1，在平面直角坐标系 $xOy$ 中，抛物线 $y = a x^{2} + bx + c (a \neq 0)$ 与 $x$ 轴交于 $A$ 、 $B$ 两点，与 $y$ 轴的负半轴交于点 $C$ ，已知抛物线的对称轴为直线 $x = \frac{\sqrt{3}}{2}$ ， $B$ 、 $C$ 两点的坐标分别为 $B (2 \sqrt{3}$ ， $0)$ ， $C (0, - 3)$ ．点 $P$ 为直线 $BC$ 下方的抛物线上的一个动点（不与 $B$ 、 $C$ 两点重合）．

（1）求此抛物线的解析式；

（2）如图1，连接 $PB$ 、 $PC$ 得到 $ΔPBC$ ，问是否存在着这样的点 $P$ ，使得 $ΔPBC$ 的面积最大？如果存在，求出面积的最大值和此时点 $P$ 的坐标；如果不存在，请说明理由．

（3）如图2，连接 $AP$ 交线段 $BC$ 于点 $D$ ，点 $E$ 为线段 $AD$ 的中点，过点 $D$ 作 $DM ⊥ AB$ 于点 $M$ ， $DN ⊥ AC$ 于点 $N$ ，连接 $EM$ 、 $EN$ ，则在点 $P$ 的运动过程中， $∠ MEN$ 的大小是否为定值？如果是，求出这个定值；如果不是，请说明理由．

如图， $AB$ 是 $⊙ O$ 的直径，点 $C$ 为 $⊙ O$ 上一点， $OE ⊥ BC$ 于点 $H$ ，交 $⊙ O$ 于点 $E$ ，点 $D$ 为 $OE$ 的延长线上一点， $DC$ 的延长线与 $BA$ 的延长线交于点 $F$ ，且 $∠ BOD = ∠ BCD$ ，连结 $BD$ 、 $AC$ 、 $CE$ ．

（1）求证： $DF$ 为 $⊙ O$ 的切线；

（2）过 $E$ 作 $EG ⊥ FD$ 于点 $G$ ，求证： $ΔCHE ≅ ΔCGE$ ；

（3）如果 $AF = 1$ ， $\sin ∠ FCA = \frac{\sqrt{3}}{3}$ ，求 $EG$ 的长．

如图，在平面直角坐标系 $xOy$ 中，已知函数 $y = \{\begin{matrix} - 3 x + m (x < 4) \\ \frac{1}{2} x - 1 (x ⩾ 4) \end{matrix}$ 的图象与双曲线 $y = \frac{k}{x} (x > 0)$ 交于 $A$ 、 $B$ 、 $C$ 三点，其中 $C$ 点的坐标为 $(6, n)$ ，且点 $A$ 的横坐标为 $\frac{4}{3}$ ．

（1）求此双曲线的解析式；

（2）求 $m$ 的值及交点 $B$ 的坐标．

某机电厂有甲乙两个发电机生产车间，甲车间每天产量为 $A$ 型发电机和 $B$ 型发电机共45台，其中 $A$ 型发电机数量比 $B$ 型发电机数量多5台．

（1）问甲车间每天生产 $A$ 、 $B$ 两种型号发电机各多少台？

（2）乙车间每天产量为50台，其中 $A$ 型发电机20台， $B$ 型发电机30台，现有一订单需 $A$ 型发电机720台和 $B$ 型发电机 $M$ 台，但由于受原材料供应限制，两车间不能同时生产，厂里决定由甲乙两车间先后用30天完成订单任务，求甲车间至少需安排生产多少天？由于甲车间还有其他生产任务，最多只能安排27天参加此订单生产，求出 $M$ 所有的可能值．

试卷网试题网古诗词网作文网范文网