通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的。下面是一个案例,请补充完整。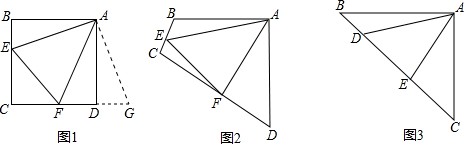
原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由。
(1)思路梳理
∵AB=CD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合。
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线。
根据 ,易证△AFG≌ ,得EF=BE+DF。
(2)类比引申
如图2,四边形ABCD中,AB=AD,∠BAD=90°,点E、F分别在边BC、CD上,∠EAF=45°。若∠B、∠D都不是直角,则当∠B与∠D满足等量关系 时,仍有EF=BE+DF。
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°。猜想BD、DE、EC应满足的等量关系,并写出推理过程。
如图是甲、乙两人同一地点出发后,路程随时间变化的图象.
(1)此变化过程中,是自变量,是因变量;
(2)甲的速度乙的速度(大于、等于、小于);
(3)6时表示;
(4)路程为150km,甲行驶了小时,乙行驶了小时;
(5)9时甲在乙的(前面、后面、相同位置);
(6)乙比甲先走了3小时,对吗?.
已知,如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠B=35°,∠C=55°
(1)求∠DAE的度数.
(2)试写出 ∠DAE与∠C-∠B有何关系?(不必证明)
如图,CD⊥AB于D,点F是BC上任意一点,FE⊥AB于E,且∠1=∠2,∠3=75°.求∠BCA的度数.
如图,一束平行光线AB与DE射向一个水平镜面后被反射,此时∠1=∠2,∠3=∠4,由此你能得到反射光线有什么位置关系?试说明你的理由. 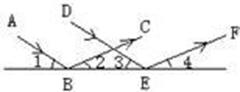
作图题.
如图,已知∠DAF,点B、C分别在AF、AD上根据要求,用尺规作图(保留作图痕迹,不写作法与证明):
(1)在AD的右侧作∠DCP=∠DAF;
(2)在射线CP上取一点E,使CE=AB,连接BE.
(3)以点A、B、E、C为顶点的四边形的形状为.