如图所示，两平行金属板E、F之间电压为U，两足够长的平行边界MN、PQ区域内，有垂直纸面向外的匀强磁场，磁感应强度为B.一质量为m、带电量为+q的粒子（不计重力），由E板中央处静止释放，经F板上的小孔射出后，垂直进入磁场，且进入磁场时与边界MN成60°角，最终粒子从边界MN离开磁场.求：
（1）粒子离开电场时的速度大小v；
（2）粒子在磁场中圆周运动的半径r和运动的时间t.
（3）两边界MN、PQ的最小距离d；
在工厂的流水线上安装水平传送带，可以把沿斜面滑下的工件用水平传送带进行传送，可大大提高工作效率。如图所示，一倾角
的光滑斜面下端与水平传送带相连，一工件从
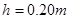高处的A点由静止滑下后到达B点的速度为
，接着以滑上水平放置的传送带。已知：传送带长
，向右保持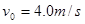
的运行速度不变，工件与传送带间的动摩擦因数
，
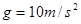，空气阻力不计，工件可看成质点。求：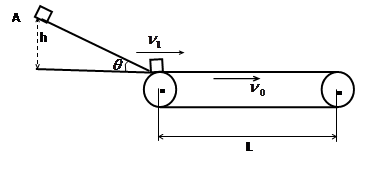
（1）求工件滑上传送带B点时的速度大小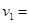
？
（2）求工件从A点由静止下滑到离开传送带C点所用的时间。
（3）假设传送带是白色的，工件为一煤块，则工件从B滑到C的过程中，在传送带上留下黑色痕迹的长度S=？
如图所示，质量为4kg的小球用细绳拴着吊在行驶的汽车后壁上，绳与竖直方向夹角为37º。已知g = 10m/s2，sin37º=0.6，cos37º=0.8，求：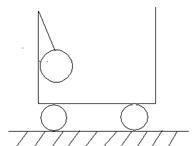
(1)汽车匀速运动时，细线对小球的拉力和车后壁对小球的压力。
(2)当汽车以a1=2m/s2向右匀减速行驶时，细线对小球的拉力和小球对车后壁的压力。
(3)当汽车以a2=10m/s2向右匀减速行驶时，细线对小球的拉力和小球对车后壁的压力。
如图所示，斜面高lm，倾角θ＝300，在斜面的顶点A以速度vo水平抛出一小球，小球刚好落于斜面底部B点，不计空气阻力，g取10m/s2，求小球抛出的速度v0和小球在空中运动的时间t。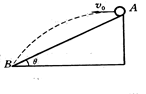
甲、乙两物体同时同地出发，沿同一方向做匀加速直线运动，它们的v-t图象如图所示。
（1）甲、乙两物体何时相遇？相遇时离出发点的距离为多少？
（2）相遇前何时甲、乙相距最远？最远距离为多少？
[物理一选修3－5]
（1）下列说法正确的是。
| A．各种原子的发射光谱都是连续谱 |
| B．爱因斯坦的光子说解释了光电效应现象，光电子的最大初动能与入射光子的频率有关 |
| C．原子核的比结合能大小可反映原子核的稳定程度，该值随质量数的增加而增大 |
| D．根据α粒子散射实验，卢瑟福提出了原子核式模型 |
E．实物粒子也具有波动性，这种与实物粒子相联系的波称为德布罗意波
（2）如图所示，一水平面上P点左侧光滑，右侧粗糙，质量为m的劈A在水平面上静止，上表面光滑，A轨道右端与水平面平滑连接，质量为M的物块B恰好放在水平面上P点，物块B与水平面的动摩擦因数为μ=0.2。一质量为m的小球C位于劈A的斜面上，距水平面的高度为h=0.9m。小球C从静止开始滑下，然后与B发生正碰（碰撞时间极短，且无机械能损失）。已知M="2" m，g=10m/s2,求：
(1)小球C与劈A分离时，C的速度大小
(2)小球C与物块B碰后的速度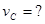
和物块B的运动时间？