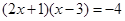2013年3月，某煤矿发生瓦斯爆炸，该地救援队立即赶赴现场进行救援，救援队利用生命探测仪在地面A、B两个探测点探测到C处有生命迹象．已知A、B两点相距4米，探测线与地面的夹角分别是30°和45°，试确定生命所在点C的深度．（精确到0.1米，参考数据：
）
如图，在Rt△ABC中，∠C=90°，∠ABC的平分线交AC于点D，点O是AB上一点，⊙O过B、D两点，且分别交AB、BC于点E、F．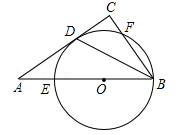
（1）求证：AC是⊙O的切线；
（2）已知AB=10，BC=6，求⊙O的半径r．
已知：如图，在同心圆中，大圆的弦AB交小圆于C、D两点．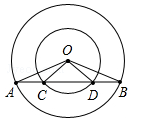
（1）求证：∠AOC=∠BOD；
（2）试确定AC与BD两线段之间的大小关系，并证明你的结论．
如图，小亮晚上在路灯下散步，已知灯杆OA=6.4m，他从灯杆底部的点O处沿直线前进9m到点D时，其影长DF=3m，当他继续前进到达点F时，其影子是变长还是变短？变化量为多少？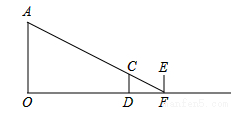
已知关于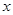
的一元二次方程
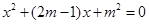有两个实数根
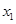和
．
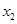（1）求实数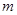
的取值范围；
（2）当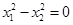
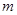时，求的值．
解下列方程（每小题3分，共9分）
（1）
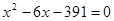
（2）
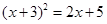
（3）