国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并对钓鱼岛进行常态化立体巡航.如图1,在一次巡航过程中,巡航飞机飞行高度为2001米,在点A测得高华峰顶F点的俯角为30°,保持方向不变前进1200米到达B点后测得F点俯角为45°,如图2.请据此计算钓鱼岛的最高海拔高度多少米.(结果保留整数,参考数值: =1.732,
=1.732, =1.414)
=1.414)
(本小题满分12分)
某县有着丰富的海产品资源. 某海产品加工企业已收购某种海产品60吨, 根据市场信息, 如果对该海产品进行粗加工, 每天可加工8吨, 每吨可获利1000元;如果进行精加工, 每天可加工2吨, 每吨可获利5000元. 由于受设备条件的限制,两种加工方式不能同时进行.(1)设精加工的吨数为
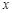 吨, 则粗加工的吨数为 吨,加工这批海产品需要天, 可获利元(用含
吨, 则粗加工的吨数为 吨,加工这批海产品需要天, 可获利元(用含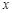 的代数式表示);
的代数式表示);(2)为了保鲜的需要, 该企业必须在两周(14天)内将这批海产品全部加工完毕,精加工的吨数
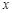 在什么范围内时, 该企业加工这批海产品的获利不低于120000元?
在什么范围内时, 该企业加工这批海产品的获利不低于120000元?
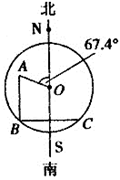
机器人“海宝”在某圆形区域表演“按指令行走”,如图所示,“海宝”从圆心O出发,先沿北偏西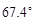 方向行走13m至A处,再沿正南方向行走14m至点B处,最后沿正东方向行走至点C处,点B、C都在圆O上。
方向行走13m至A处,再沿正南方向行走14m至点B处,最后沿正东方向行走至点C处,点B、C都在圆O上。(1)求弦BC的长;
(2)求圆O的半径。(本题参考数据:
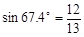 ,
,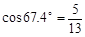 ,
,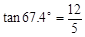 )
)
已知关于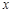 的一元二次方程
的一元二次方程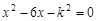 (k为常数)
(k为常数)(1)求证:方程有两个不相等的实数根。
(2)设
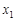 、
、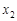 为方程的两个实数根,且
为方程的两个实数根,且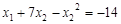 试求k的值。
试求k的值。
水是生命之源。长期以来,某市由于水价格不合理,一定程度上造成了水资源的浪费。为改善这一状况,相关部门正在研究制定居民用水价格调整方案。小明想为政府决策提供信息,于是在某小区内随机访问了部分居民,就每月的用水量、可承受的水价调整的幅度等进行调查,并把调查结果整理成图a、图b.
已知被调查居民每户每月的用水量在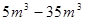 之间,被调查的居民中对居民用水价格调价幅度抱“无所谓”态度的有8户,试回答下列问题:
之间,被调查的居民中对居民用水价格调价幅度抱“无所谓”态度的有8户,试回答下列问题: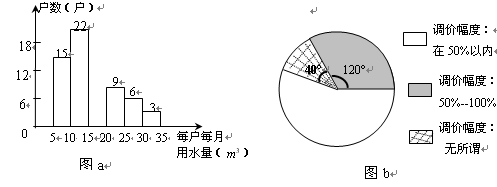
(1)图a使用的统计图表的名称是 ,它是表示一组数据 的量;(填“平均水平”、“离散程度”或“分布情况”)
(2)上述两个统计图表是否完整,若不完整,试把它们补全;
(3)若采用阶梯式累进制调价方案(如表1所示),试估计该小区有百分之几的居民用水费用的增长幅度不超过50%?
|
先阅读读短文,再解答短文后面的问题: 在几何学中,通常用点表示位置,用线段的长度表示两点间的距离,用一条射线表示一个方向。在线段的两个端点中(如图),如果我们规定一个顺序:
在几何学中,通常用点表示位置,用线段的长度表示两点间的距离,用一条射线表示一个方向。在线段的两个端点中(如图),如果我们规定一个顺序: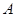 为始点,
为始点,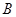 为终点,我们就说线段
为终点,我们就说线段 具有射线的
具有射线的 方向,线段
方向,线段 叫做有向线段,记作
叫做有向线段,记作 ,线段
,线段 的长度叫做有向线段
的长度叫做有向线段 的长度(或模),记作
的长度(或模),记作 。
。
有向线段包含三个要素:始点、方向和长度,知道了有向线段的始点,它的终点就被方向和长度一确定。解答下列问题: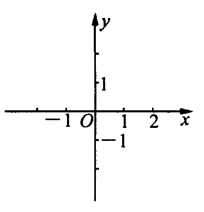
(1)在平面直角坐标系中画出有向线段
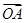 (有向线段与
(有向线段与 轴的长度单位相同),
轴的长度单位相同),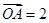 ,
,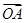 与
与 轴的正半轴的夹角是
轴的正半轴的夹角是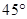 ,且与
,且与 轴的正半轴的夹角是
轴的正半轴的夹角是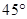 ;
;(2)若
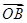 的终点
的终点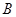 的坐标为(3,
的坐标为(3, ),求它的模及它与
),求它的模及它与 轴的正半轴的夹角
轴的正半轴的夹角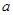 的度数。
的度数。