某中学为了预测本校应届毕业女生“一分钟跳绳”项目考试情况,从九年级随机抽取部分女生进行该项目测试,并以测试数据为样本,绘制出如图所示的部分频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值)和扇形统计图.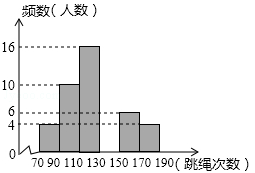

根据统计图提供的信息解答下列问题:
(1)补全频数分布直方图,并指出这个样本数据的中位数落在第 小组;
(2)若测试九年级女生“一分钟跳绳”次数不低于130次的成绩为优秀,本校九年级女生共有260人,请估计该校九年级女生“一分钟跳绳”成绩为优秀的人数;
(3)如测试九年级女生“一分钟跳绳”次数不低于170次的成绩为满分,在这个样本中,从成绩为优秀的女生中任选一人,她的成绩为满分的概率是多少?
计算: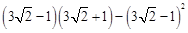
如图1,在Rt△ABC中,∠C=90°,AC=9cm,BC=12cm.在Rt△DEF中,∠DFE=90°,EF=6cm,
DF=8cm.E,F两点在BC边上,DE,DF两边分别与AB边交于G,H两点.现固定△ABC不动,△DEF从点F
与点B重合的位置出发,沿BC以1cm/s的速度向点C运动,点P从点F出发,在折线FD—DE上以2cm/s的速
度向点E运动.△DEF与点P同时出发,当点E到达点C时,△DEF和点P同时停止运动.设运动的时间是
t(单位:s),t>0.
(1)当t=2时,PH=cm ,DG =cm;
(2)t为多少秒时△PDE为等腰三角形?请说明理由;
(3)t为多少秒时点P与点G重合?写出计算过程;
(4)求tan∠PBF的值(可用含t的代数式表示).
矩形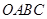 在平面直角坐标系中位置如图所示,
在平面直角坐标系中位置如图所示,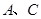 两点的坐标分别为
两点的坐标分别为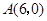 ,
,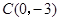 ,直线
,直线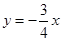 与
与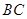 边相交于
边相交于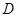 点.
点.
(1)求点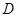 的坐标;
的坐标;
(2)若抛物线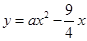 经过点
经过点 ,试确定此抛物线的表达式;
,试确定此抛物线的表达式;
(3)设(2)中的抛物线的对称轴与直线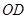 交于点
交于点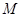 ,点
,点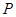 为对称轴上一动点,以
为对称轴上一动点,以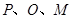 为顶点的三角形与
为顶点的三角形与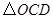 相似,求符合条件的点
相似,求符合条件的点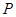 的坐标.
的坐标.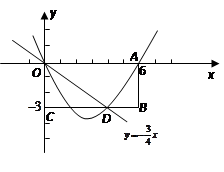
如图,扇形OAB的半径OA=3,圆心角∠AOB=90°,点C是弧AB上异于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连结DE,点G、H在线段DE上,且DG=GH=HE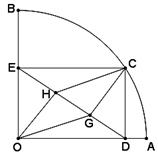
(1)求证:四边形OGCH是平行四边形;
(2)当点C在弧AB上运动时,在CD、CG、DG中,是否存在长度不变的线段?若存在,请求出该线段的长度;
(3)求证: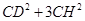 是定值.
是定值.
某花圃用花盆培育某种花苗,经过试验发现每盆的盈利与每盆的株数构成一定的关系,每盆植入3株时,平均单株盈利3元,以同样的栽培条件,若每盆增加1株,平均单株盈利就减少0.5元,要使每盆的盈利达到10元,每盆应该植多少株?