已知:关于x的二次函数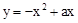 (a>0),点A(n,y1)、B(n+1,y2)、C(n+2,y3)都在这个二次函数的图象上,其中n为正整数.
(a>0),点A(n,y1)、B(n+1,y2)、C(n+2,y3)都在这个二次函数的图象上,其中n为正整数.
(1)y1=y2,请说明a必为奇数;
(2)设a=11,求使y1≤y2≤y3成立的所有n的值;
(3)对于给定的正实数a,是否存在n,使△ABC是以AC为底边的等腰三角形?如果存在,求n的值(用含a的代数式表示);如果不存在,请说明理由.
(本小题满分8分)
已知,在△ABC中,∠BAC=90°,AB=AC,BC= ,点D、E在BC边上(均不与点B、C重合,点D始终在点E左侧),且∠DAE=45°.
,点D、E在BC边上(均不与点B、C重合,点D始终在点E左侧),且∠DAE=45°.(1)请在图①中找出两对相似但不全等的三角形,写在横线上,;
(2)设BE=m,CD=n,求m与n的函数关系式,并写出自
 变量n的取值范围;
变量n的取值范围;(3)如图②,当BE=CD时,求DE的长;
(4)求证:无论BE与CD是否相等,都有DE2=BD2+CE2.

(本小题满分6分)
如图,在△ABC中,∠ACB=90°,O为BC边上一点,以O为圆心,OB为半径作半圆与AB边和BC边分别交于点D、点E,连接CD,且CD=CA,BD= ,tan∠ADC=2.
,tan∠ADC=2.
(1)求证:CD是半圆O的切线
(2)求半圆O的直径;
(3)求AD的长.
(本小题满分6分)
某超市销售一款进价为50元/个的书包,物价部门规定这款书包的售价不得高于70元/个,市场调查发现:以60元/个的价格销售,平均每周销售书包100个;若每个书包的销售价格每提高1元,则平均每周少销售书包2个.(1)求该超市这款书包平均每周的销售量y(个)与销售价x(元/个)之间的函数关系式;
(2)求该超市这款书包平均每周的销售利润w(元)与销售价x(元/个)之间的函数关系式;
(3)当每个书包的销售价为多少元时,该超市这款书包平均每周的销售利润最大?最
 大利润是多少元?
大利润是多少元?
(本小题满分5分)已知抛物线 与
与 轴交于A、B两点(点A在点B左侧),且对称轴为x=-1.
轴交于A、B两点(点A在点B左侧),且对称轴为x=-1.(1)求
 的值;
的值;(2)画出这条抛物线;
(3)若直线
 过点B且与抛物线交于点
过点B且与抛物线交于点 (-2m,-3m),根据图象回答:当
(-2m,-3m),根据图象回答:当 取什么值时,
取什么值时, ≥
≥ .
.
(本小题满分5分)
小红在学习了教科书上相关内容后自制了一个测角仪(图①),并尝试用它来测量校园内一座教学楼CD的高度(如图②).她先在A处测得楼顶C的仰角 30°,再向楼的方向直行10米到达B处,又测得楼顶C的仰角
30°,再向楼的方向直行10米到达B处,又测得楼顶C的仰角 60°,若小红的目高(眼睛到地面的高度)AE为1.60米,请你帮助她计算出这座教学楼CD的高度(结果精确到0.1米,参考数据:
60°,若小红的目高(眼睛到地面的高度)AE为1.60米,请你帮助她计算出这座教学楼CD的高度(结果精确到0.1米,参考数据: ,
, ,
, ).
).