如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数 的图象经过点M,N.
的图象经过点M,N.
(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM= .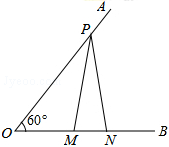
某旅行社组织一批游客外出旅游,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满.已知45座客车租金为每辆220元,60座客车租金为每辆300元,问:
(1)这批游客的人数是多少?原计划租用多少辆45座客车?
(2)若租用同一种车,要使每位游客都有座位,应该怎样租用才合算?
广安市积极开展“阳光体育进校园”活动,各校学生坚持每天锻炼一小时.某校根据实际,决定主要开设A:乒乓球,B:篮球,C:跑步,D:跳绳四种运动项目.为了解学生最喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图.请你结合图中信息解答下列问题.
(1)样本中最喜欢B项目的人数百分比是________,其所在扇形图中的圆心角的度数是____;
(2)请把统计图补充完整;
(3)已知该校有1200人,请根据样本估计全校最喜欢乒乓球的人数是多少?
如图所示,△A′B′C′是△ABC经过平移得到的,A(﹣4,﹣1),B(﹣5,﹣4),C(﹣1,﹣3),△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).
(1)请写出三角形ABC平移的过程;
(2)分别写出点A′,B′,C′的坐标;
(3)求△A′B′C′的面积.
如图,已知∠1=∠2,∠C=∠D,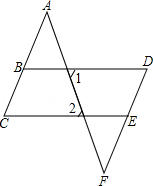
求证:∠A=∠F.