如图，抛物线y=ax2+bx+3与x轴相交于点A（﹣1，0）、B（3，0），与y轴相交于点C，点P为线段OB上的动点（不与O、B重合），过点P垂直于x轴的直线与抛物线及线段BC分别交于点E、F，点D在y轴正半轴上，OD=2，连接DE、OF．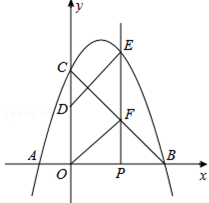
（1）求抛物线的解析式；
（2）当四边形ODEF是平行四边形时，求点P的坐标；
（3）过点A的直线将（2）中的平行四边形ODEF分成面积相等的两部分，求这条直线的解析式．（不必说明平分平行四边形面积的理由）
网格中有一个小甲虫（
），它喜欢吃牛粪，它又会把吃剩的牛粪滚成牛粪球（
）藏进仓库（
）.规定向左为L，向右为R，向上为U，向下D，如：L1表示向左平移一格，D2表示向下平移2格.例如：要把左图中的所有的牛粪球推到最近的仓库里，可以编写程序：L1-R1-U2-D3-R2-U1，小甲虫就能把所有的牛粪球推到最近的仓库.你来试一试，可编写一个怎样的程序才能使小甲虫把右边图上的所有牛粪球推到最近的仓库里.（只需写出一种可行的程序即可）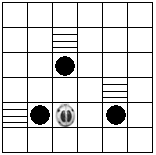
学校对学生寝室进行了整顿，并举行了文明寝室评比，结果七年级（3）班被评为文明寝室.你看她们的牙刷、牙杯放得多整齐，你能说说她们用了数学中的什么知识？
举一个生活中平移的例子.
已知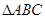
，以直线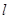
为对称轴，将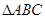作轴对称变换，请画出经变换后的图形.（请保留作图痕迹）
画出下图的所有对称轴：