有下列四个命题:
①对于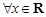 ,函数
,函数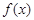 满足
满足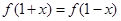 ,则函数
,则函数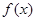 的最小正周期为2;
的最小正周期为2;
②所有指数函数的图象都经过点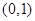 ;
;
③若实数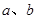 满足
满足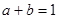 ,则
,则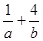 的最小值为9;
的最小值为9;
④已知两个非零向量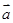 ,
, ,则“
,则“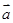
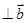 ”是“
”是“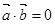 ”的充要条件.
”的充要条件.
其中真命题的个数为( )
| A.0 | B.1 | C.2 | D.3 |
对于函数 与
与 和区间D,如果存在
和区间D,如果存在 ,使
,使 ,则称
,则称 是函数
是函数 与
与 在区间D上的“友好点”.现给出两个函数:
在区间D上的“友好点”.现给出两个函数:
① ,
, ;
;
② ,
, ;
;
③ ,
, ;
;
④
 ,
, ,
,
则在区间 上的存在唯一“友好点”的是()
上的存在唯一“友好点”的是()
| A.①② | B.③④ | C.②③ | D.①④ |
对于任意给定的实数 ,直线
,直线 与双曲线
与双曲线 ,
, 最多有一个交点,则双曲线的离心率等于()
最多有一个交点,则双曲线的离心率等于()
A. |
B. |
C. |
D. |
已知点 是△
是△ 所在平面内的一点,边AB的中点为D,若
所在平面内的一点,边AB的中点为D,若 ,其中
,其中 ,则点
,则点 一定在()
一定在()
| A.AB边所在的直线上 | B.BC边所在的直线上 |
| C.AC边所在的直线上 | D.△ 的内部 的内部 |
设 则
则 中奇数的个数为( )
中奇数的个数为( )
| A.2 | B.3 | C.4 | D.5 |
已知等比数列 的公比
的公比 ,且
,且 成等差数列,则
成等差数列,则 的前8项和为( )
的前8项和为( )
| A.127 | B.255 | C.511 | D.1023 |