如图，在平面直角坐标系中，反比例函数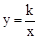
(x>0)的图象和矩形ABCD的第一象限，AD平行于x轴，且AB=2，AD=4，点A的坐标为(2，6) ．
（1）直接写出B、C、D三点的坐标；
（2）若将矩形向下平移，矩形的两个顶点恰好同时落在反比例函数的图象上，猜想这是哪两个点，并求矩形的平移距离和反比例函数的解析式．
如图，反比例函数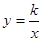
（x＞0）的图象过点A 。
求反比例函数的解析式；
若点B在
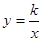（x＞0）的图象上，求直线AB的解析式．
如图，点A、D、F、B在同一条直线上，AD=BF，AE=BC，且AE∥BC.
求证：EF∥CD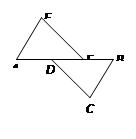
如图，AD为△ABC的中线，BE为△ABD的中线。
（1）∠ABE=15°，∠BAD=40°，求∠BED的度数；
（2）在△BED中作BD边上的高；
（3）若△ABC的面积为40，BD=5，则△BDE 中BD边上的高为多少？
如图，已知直线AE∥BF，∠EAC=28°，∠FBC=50°，求∠ACB的度数.
如图，直线AD与AB、CD相交于A、D两点，EC、BF与AB、CD相交于E、C、B、F，如果∠1=∠2，∠B=∠C．
求证：∠A=∠D．