如图,在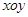 平面第一象限整个区域分布匀强电场,电场方向平行
平面第一象限整个区域分布匀强电场,电场方向平行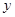 轴向下,在第四象限内存在有界匀强磁场,左边界为
轴向下,在第四象限内存在有界匀强磁场,左边界为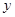 轴,右边界为
轴,右边界为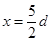 的直线,磁场方向垂直纸面向外。质量为
的直线,磁场方向垂直纸面向外。质量为 、带电量为
、带电量为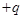 的粒子从
的粒子从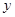 轴上
轴上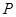 点以初速度
点以初速度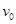 垂直
垂直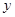 轴射入匀强电场,在电场力作用下从
轴射入匀强电场,在电场力作用下从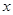 轴上
轴上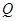 点以与
点以与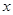 轴正方向成45°角进入匀强磁场。已知
轴正方向成45°角进入匀强磁场。已知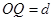 ,不计粒子重力。求:
,不计粒子重力。求: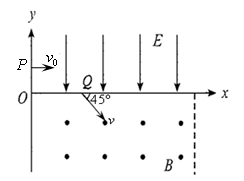
(1)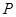 点坐标;
点坐标;
(2)要使粒子能再进入电场,磁感应强度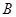 的取值范围;
的取值范围;
(3)要使粒子能第二次进入磁场,磁感应强度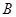 的取值范围。
的取值范围。
一单摆在地面处的摆动周期与在某矿井底部摆动周期的比值为k.设地球的半径为R.假定地球的密度均匀,已知质量均匀分布的球壳对壳内物体的引力为零.求矿井的深度d.
如图所示,光滑绝缘竖直细杆与以正点电荷O为圆心的圆周交于B、C两点。一质量m、带电量为-q的空心小球从杆上A点无初速下落。设AB =" BC" = h,小球滑到B点的速度为 试求:
试求:
(1)小球滑至C点的速度;
(2)A、C两点的电势差。
一列简谐横波上有相距4m的A、B两点,波的传播方向是由A向B,波长大于2m,如图所示的是A、B两质点的振动图象,求这列波可能的波速.
如图所示,与水平面成θ=37°的粗糙斜面与一光滑圆轨道相切于A点,斜面AB的长度s=2.3 m,动摩擦因数μ=0.5,圆轨道半径为R=0.6m。让质量为m=1kg物体(可视为质点)从B点以某一沿斜面向下的初速度释放,恰能沿轨道运动到圆轨道的最高点C,空气阻力忽略不计。(取sin37°=0.6,cos37°=0.8)
(1)求释放时的初动能;
(2)设物体从C点落回斜面AB上的P点,试通过计算判断P位置比圆心O高还是低.
一滑块(可视为质点)经水平轨道AB进入竖直平面内的四分之一圆弧形轨道BC.已知滑块的质量m=0.50kg,滑块经过A点时的速度vA=5.0m/s,AB长x=4.5m,滑块与水平轨道间的动摩擦因数μ=0.10,圆弧形轨道的半径R=0.50m,滑块离开C点后竖直上升的最大高度h=0.10m.取g=10m/s2.求:
(1)滑块第一次经过B点时速度的大小;
(2)滑块刚刚滑上圆弧形轨道时,对轨道上B点压力的大小;
(3)滑块在从B运动到C的过程中克服摩擦力所做的功.