某电子元件厂准备生产4600个电子元件，甲车间独立生产了一半后，由于要尽快投入市场，乙车间也加入该电子元件的生产，若乙车间每天生产的电子元件是甲车间的1.3倍，结果用33天完成任务，问甲车间每天生产电子元件多少个？在这个问题中设甲车间每天生产电子元件x个，根据题意可得方程为
A． |
B． |
C． |
D． |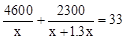
关于x的方程3x＋2＝x－4b 的解是5，则b＝( )
| A．－1 | B．－2 | C．2 | D．－3 |
已知当
时，代数式
值为6，那么当
时，代数式值为（）
| A．2 | B．3 | C．-4 | D．-5 |
长方形的一边长等于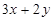
，另一边长比它长
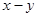，这个长方形的周长是（）
A． |
B． |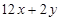
C． |
D． |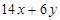
若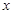
表示一个两位数，把数字3放在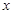的左边，组成一个三位数是（）
A． |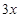
B． |
C． |
D． |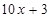
下列说法中正确的有（）
①若两数的差是正数，则这两个数都是正数；
②任何数的绝对值一定是正数；
③零减去任何一个有理数，其差是该数的相反数；
④在数轴上与原点距离越远的点表示的数越大．
⑤正数的倒数是正数，负数的倒数是负数，任何数都有倒数．
| A．0个 | B．1个 | C．2个 | D．3个 |