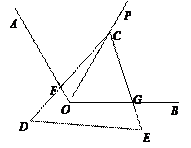如图，在活动课上，小明和小红合作用一副三角板来测量学校旗杆高度．已知小明的眼睛与地面的距离（AB）是1.7m，他调整自己的位置，设法使得三角板的一条直角边保持水平，且斜边与旗杆顶端M在同一条直线上，测得旗杆顶端M仰角为45°；小红的眼睛与地面的距离（CD）是1.5m，用同样的方法测得旗杆顶端M的仰角为30°．两人相距28米且位于旗杆两侧（点B、N、D在同一条直线上）．求出旗杆MN的高度．（参考数据：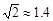
，
，结果保留整数．）
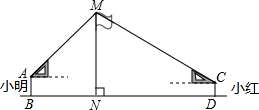
解方程组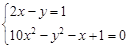
解下列分式方程：
(1)
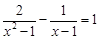； (2)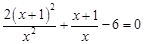
．
如图，在直角坐标系xOy中，点A在x轴的正半轴上，点B在y轴的正半轴上, 以OB为直径的⊙C与AB交于点D， DE与⊙C相切交x轴于点E, 且OA=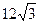
cm，∠OAB="30°."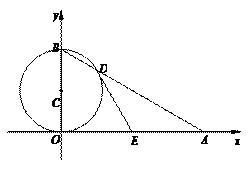 
（1）求点B的坐标及直线AB的解析式;
（2）过点B作BG^EC于 F, 交x轴于点G, 求BD的长及点F的坐标;
（3）设点P从点A开始沿A
BG的方向以4cm/s的速度匀速向点G移动，点Q同时
从点A开始沿AG匀速向点G移动, 当四边形CBPQ为平行四边形时, 求点Q的移动
速度.
已知关于x的两个一元二次方程：
方程①: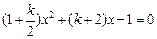 
; 方程②: 
.
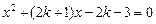（1）若方程①有两个相等的实数根，求解方程②；
（2）若方程①和②中只有一个方程有实数根, 请说明此时哪个方程没有实数根, 并化
简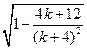
；
（3）若方程①和②有一个公共根a, 求代数式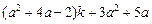
的值．
已知△DCE的顶点C在ÐAOB的平分线OP上，CD交OA于F, CE交OB于G.
（1）如图1，若CD^ OA, CE^OB, 则图中有哪些相等的线段, 请直接写出你的结论:
；
（2）如图2, 若ÐAOB=120°, ÐDCE =ÐAOC, 试判断线段CF与线段CG的数量关系并
加以证明；
（3）若ÐAOB=a，当ÐDCE满足什么条件时，你在（2）中得到的结论仍然成立, 请
直接写出ÐDCE满足的条件.