如图,已知抛物线 与直线
与直线 交于点O(0,0),
交于点O(0,0), 。点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E。
。点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E。
(1)求抛物线的函数解析式;
(2)若点C为OA的中点,求BC的长;
(3)以BC,BE为边构造条形BCDE,设点D的坐标为(m,n),求m,n之间的关系式。
如图,已知直线AB与x轴交于A(6,0)点,与y轴交于B(0,10)点,点M的坐标为(0,4),
点P(x,y)是折线O→A→B的动点(不与O点、B点重合),连接OP、MP,设△OPM的面积为S.
(1) 求S关于x的函数表达式,并写x的取值范围;
(2) 当△OPM是以OM为底边的等腰三角形时,求S的值;
(3) 当线段MP分△OAB的面积比为1∶4时,求P点坐标.
2008年6月1日起,我国实施“限塑令”,开始有偿使用环保购物袋.为了满足市场需求,某厂家生产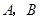 两种款式的布质环保购物袋,每天共生产4500个,两种购物袋的成本和售价如下表,设每天生产
两种款式的布质环保购物袋,每天共生产4500个,两种购物袋的成本和售价如下表,设每天生产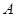 种购物袋
种购物袋 个,每天共获利
个,每天共获利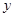 元.
元.
(1)求出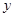 与
与 的函数关系式;
的函数关系式;
(2)如果该厂每天最多投入成本10000元,那么每天最多获利多少?
有甲、乙两个蓄水池,现将甲池中的水匀速注入乙池。甲、乙两个蓄水池中水的深度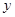 (米)与注水时间
(米)与注水时间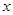 (小时)之间的关系如图所示,根据图像提供的信息,回答下列问题:
(小时)之间的关系如图所示,根据图像提供的信息,回答下列问题:
(1)注水前甲池中水的深度是_____________米。(直接写出答案)。
(2)求甲池中水的深度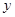 (米)与注水时间
(米)与注水时间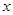 (小时)之间的函数关系式;
(小时)之间的函数关系式;
(3)求注水多长时间时,甲、乙两个蓄水池中水的深度相同。
已知一次函数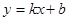 的图象经过点A(-2,-3)及点B(1,6).
的图象经过点A(-2,-3)及点B(1,6).
(1)求此一次函数的解析式.
(2)判断点C( ,2)是否在函数的图象上.
,2)是否在函数的图象上.
已知:如图,AB=CD,DE⊥AC,BF⊥AC,E,F是垂足, .求证:
.求证: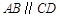 .
.