一个盒子里有3个分别标有号码为1,2,3的小球,每次取出一个,记下它的标号后再放回盒子中,共取3次,则取得小球标号最大值是3的取法有( )
| A.12种 | B.15种 | C.17种 | D.19种 |
已知直线 及
及 与函数
与函数 图像的交点分别为
图像的交点分别为 ,与函数
,与函数 图像的交点分别为
图像的交点分别为 ,则直线AB与CD()
,则直线AB与CD()
| A.相交,且交点在第I象限 | B.相交,且交点在第II象限 |
| C.相交,且交点在第IV象限 | D.相交,且交点在坐标原点 |
已知点 、
、 分别为双曲线
分别为双曲线 :
:
 的左焦点、右顶点,点
的左焦点、右顶点,点 满足
满足 ,则双曲线的离心率为()
,则双曲线的离心率为()
A. |
B. |
C. |
D. |
已知 ,则“
,则“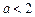 ”是“
”是“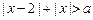 恒成
恒成
立”的()
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
设函数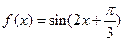 ,则下列结论正确的是()
,则下列结论正确的是()
A.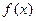 的图像关于直线 的图像关于直线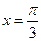 对称 对称 |
B.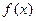 的图像关于点 的图像关于点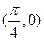 对称 对称 |
C.把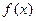 的图像向左平移 的图像向左平移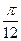 个单位,得到一个偶函数的图像 个单位,得到一个偶函数的图像 |
|
D.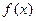 的最小正周期为 的最小正周期为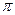 ,且在 ,且在 上为增函数 上为增函数 |
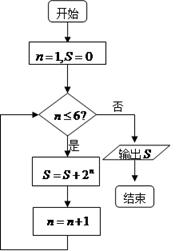
若右面的程序框图输出的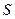 是
是 ,则①应为()
,则①应为()
A. ? ? |
B. ? ? |
C.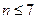 ? ? |
D.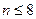 ? ? |