如图所示,装置BO′O可绕竖直轴O′O转动,可视为质点的小球A与两细线连接后分别系于B、C两点,装置静时细线AB水平,细线AC与竖直方向的夹角θ=37º。已知小球的质量m=1kg,细线AC长L=1m,B点距C点的水平和竖直距离相等。(重力加速度g取10m/s2,sin37º=0.6,cos37º=0.8)

(1)若装置匀速转动的角速度为ω1时,细线AB上的张力为0而细线AC与竖直方向的夹角仍为37°,求角速度ω1的大小;
(2)若装置匀速转动的角速度为ω2时,细线AB刚好竖直,且张力为0,求此时角速度ω2的大小;
(3)装置可以以不同的角速度匀速转动,试通过计算在坐标图中画出细线AC上张力T随角速度的平方ω2变化的关系图像
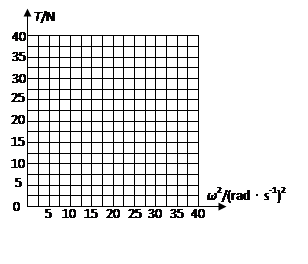
2007年10月24日18时05分,中国第一颗探月卫星“嫦娥一号”在西昌卫星发射中心成功升空,“嫦娥奔月”成为中国航天的现实. 为了方便研究,我们将“嫦娥奔月”的过程简化为:“嫦娥一号”升空后,首先进入周期为T1的近地圆轨道,然后在地面的指令下经过一系列的变轨后最终被月球捕获,在距离月球表面为h的轨道上绕月球做匀速圆周运动. 已知地球质量为M1,半径为R1,月球质量为M2,半径为R2。求:“嫦娥一号”绕月球运动时的周期T2(最终结果用题目中的物理量来表示).
滑板运动是一项非常刺激的水上运动,研究表明,在进行滑板运动时,水对滑板的作用力Fx垂直于板面,大小为kv2,其中v为滑板速率(水可视为静止)。某次运动中,在水平牵引力作用下,当滑板和水面的夹角θ=37°时,滑板做匀速直线运动,相应的k="54" kg/m,人和滑板的总质量为108 kg,试求(重力加速度g取10 m/s2,sin 37°=0.6,忽略空气阻力):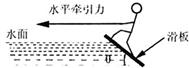
(1)水平牵引力的大小;
(2)滑板的速率;
如图,质量为m的b球用长h的细绳悬挂于水平轨道BC的出口C处。质量也为m的小球a,从距BC高h的A处由静止释放,沿ABC光滑轨道滑下,在C处与b球正碰并与b粘在一起。已知BC轨道距地面有一定的高度,悬挂b球的细绳能承受的最大拉力为2.8mg。试问:
①a与b球碰前瞬间的速度多大?
②a、b两球碰后,细绳是否会断裂?(要求通过计算回答)
以下两小题中任选一题做。
|
(1)如图所示是一列沿x轴正方向传播的简谐横波在t =0时刻的波形图,波的传播速度v = 2m/s,试求:
①x =" 4" m处质点的振动函数表达式
如右图所示,一辆上表面光滑的平板小车长L=2 m,车上左侧有一挡板,紧靠挡板处有一可看成质点的小球.开始时,小车与小球一起在水平面上向右做匀速运动,速度大小为v0=5 m/s.某时刻小车开始刹车,加速度大小a=4 m/s2.经过一段时间,小球从小车右端滑出并落到地面上.求: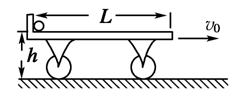
(1)从刹车开始到小球离开小车所用的时间;
(2)小球离开小车后,又运动了t1=0.5 s落地.小球落地时落点离小车右端多远?