某一长直的赛道上，有一辆F1赛车，前方200m处有一安全车正以
的速度匀速前进，这时赛车从静止出发以
的加速度追赶；求：
（1）赛车出发多长时间追上安全车？（ 5分）
（2）当赛车刚追上安全车时，赛车手立即刹车，使赛车以
的加速度做匀减速直线运动，再经过多长时间两车第二次相遇？
(选修模块3-3)(12分)
某学习小组做了如下实验：先把空的烧瓶放入冰箱冷冻，取出烧瓶，并迅速把一个气球紧套在烧瓶颈上，封闭了一部分气体，然后将烧瓶放进盛满热水的烧杯里，气球逐渐膨胀起来，如图。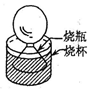
(1)(4分)在气球膨胀过程中，下列说法正确的是．
| A．该密闭气体分子间的作用力增大 |
| B．该密闭气体组成的系统熵增加 |
| C．该密闭气体的压强是由于气体重力而产生的 |
| D．该密闭气体的体积是所有气体分子的体积之和 |
(2)(4分)若某时刻该密闭气体的体积为V，密度为ρ，平均摩尔质量为M，阿伏加德罗常数为NA，则该密闭气体的分子个数为；
(3)(4分)若将该密闭气体视为理想气体，气球逐渐膨胀起来的过程中，气体对外做了0.6J的功，同时吸收了0.9J的热量，则该气体内能变化了J；若气球在膨胀过程中迅速脱离瓶颈，则该气球内气体的温度(填“升高”或“降低”)。
(18分)如图所示，劲度系数k＝100N/m的一根轻质弹簧，右端固定在竖直墙壁上，左端连接一质量m＝1.0kg的小物块，开始时弹簧处于原长，小物块静止于O点，现将小物块缓慢向左拉动至A点后释放，让小物块沿水平面向右运动起来，已知OA长度L＝0.25m，小物块与水平面间的动摩擦因数μ＝0.1，最大静摩擦力可看成等于滑动摩擦力的大小，g取10m/s2。
⑴试在坐标纸中作出小物块在由O移动到A的过程中，弹簧弹力F随伸长量x变化的F-x图象，类比于由v-t图象求位移的方法，求此过程中克服弹簧弹力做的功W；
⑵求小物块从A点向右运动过程中的最大速度v；
⑶求小物块从A点开始运动后，第一次到达最右端时，弹簧的形变量；
⑷求小物块从A点开始运动直至静止的总路程。
(16分)如图所示，让一可视为质点的小球从光滑曲面轨道上的A点无初速滑下，运动到轨道最低点B后，进入半径为R的光滑竖直圆轨道，并恰好通过轨道最高点C，离开圆轨道后继续在光滑平直轨道上运动到D点后抛出，最终撞击到搁在轨道末端点和水平地面之间的木板上，已知轨道末端点距离水平地面的高度为H＝0.8m，木板与水平面间的夹角为θ＝37°，小球质量为m＝0.1kg，A点距离轨道末端竖直高度为h＝0.2m，不计空气阻力。(取g＝10m/s2，sin37°＝0.6，cos37°＝0.8)
⑴求圆轨道半径R的大小；
⑵求小球从轨道末端点冲出后，第一次撞击木板时的位置距离木板上端的竖直高度有多大；
⑶若改变木板的长度，并使木板两端始终与平台和水平面相接，试通过计算推导小球第一次撞击木板时的动能随木板倾角θ变化的关系式，并在图中作出Ek-(tanθ)2图象。
(14分)如图所示，质量为m＝2kg的小球穿在长L＝1m的轻杆顶部，轻杆与水平方向成θ＝37°的夹角，将小球由静止释放，1s后小球恰好到达轻杆底端，取g＝10m/s2，sin37°＝0.6，cos37°＝0.8，求：
⑴小球到达杆底时重力对它做功的功率；
⑵小球与轻杆之间的动摩擦因数μ；
⑶若在竖直平面内对小球施加一个垂直于轻杆方向的恒力F，小球从静止释放后，将以大小为1m/s2的加速度向下运动，则恒力F大小为多大？
(12分)如图所示，一长为L的长方形木块在水平地面上由静止开始以加速度a做匀加速直线运动，先后经过A、B两点位置，且通过A、B两点所用的时间分别为t1和t2，求：
⑴木块分别通过位置A、B的平均速度大小；
⑵木块前端P点到达位置A时的瞬时速度；
⑶木块前端P在A、B之间运动所需的时间。