如图所示，在坐标系xOy中，y轴右侧有一匀强电场；在第二、三象限内有一有界匀强磁场，其上、下边界无限远，右边界为y轴、左边界为平行于y轴的虚线，磁场的磁感应强度大小为B，方向垂直纸面向里。一带正电，电量为q、质量为m的粒子以某一速度自磁场左边界上的A点射入磁场区域，并从O点射出，粒子射出磁场的速度方向与x轴的夹角θ＝45°，大小为v．粒子在磁场中的运动轨迹为纸面内的一段圆弧，且弧的半径为磁场左右边界间距的
倍。粒子进入电场后，在电场力的作用下又由O点返回磁场区域，经过一段时间后再次离开磁场。已知粒子从A点射入到第二次离开磁场所用的时间恰好等于粒子在磁场中做圆周运动的周期。忽略重力的影响。求：
（1）粒子经过A点时速度的方向和A点到x轴的距离；
（2）匀强电场的大小和方向；
（3）粒子从第二次离开磁场到再次到达磁场所用的时间。
某研究性学习小组首先根据小孔成像原理估测太阳半径，再利用万有引力定律估算太阳的密度.准备的器材有:①不透光圆筒，一端封上不透光的厚纸，其中心扎一小孔，另一端封上透光的薄纸；②毫米刻度尺.已知地球绕太阳公转的周期为T，万有引力常量为G.要求:(1)简述根据小孔成像原理估测太阳半径R的过程.(2)利用万有引力定律推算太阳密度.
如图所示，两根足够长的直金属导轨MN、PQ平行放置在倾角为θ的绝缘斜面上，两导轨间距为L。M、P两点间接有阻值为R的电阻。一根质量为m的均匀直金属杆ab放在两导轨上，并与导轨垂直。整套装置处于匀强磁场中，磁场方向垂直于斜面向上。导轨和金属杆的电阻可忽略。让金属杆ab沿导轨由静止开始下滑，经过足够长的时间后，金属杆达到最大速度vm，在这个过程中，电阻R上产生的热为Q。导轨和金属杆接触良好，它们之间的动摩擦因数为μ，且μ<tanθ。已知重力加速度为g。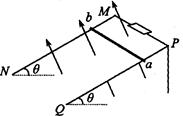
(1)求磁感应强度的大小；
(2)金属杆在加速下滑过程中，当速度达到
时，求此时杆的加速度大小；
(3)求金属杆从静止开始至达到最大速度的过程中下降的高度。
发电站通过升压变压器、输电导线和降压变压器把电能输送到用户,如果升压变压器和降压变压器都可视为理想变压器。如图所示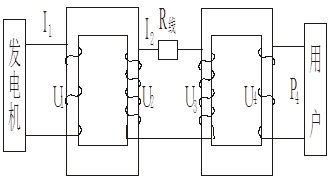
(1)若发电机的输出功率是 100 kW,输出电压是250 V,升压变压器的原、副线圈的匝数比为 1∶25,求升压变压器的输出电压和输电导线中的电流；
(2)若输电导线中的电功率损失为输入功率的 4%,求输电导线的总电阻和降压变压器原线圈两端的电压。
如图所示，放置在水平面内的平行金属框架宽为L=0.4m，金属棒ab置于框架上，并与两框架垂直，整个框架位于竖直向下、磁感强度B=0.5T的匀强磁场中，电阻R=0.09Ω，ab的电阻r=0.01Ω，摩擦不计，当ab在水平恒力F作用下以v=2.5m/s的速度向右匀速运动时，求: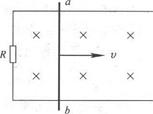
(1) 回路中的感应电流的大小；
(2) 恒力F的大小；
(3) 电阻R上消耗的电功率.
如图，体积为V、内壁光滑的圆柱形导热气缸顶部有一质量和厚度均可忽略的活塞；气缸内密封有温度为2.4T0、压强为1.2P0的理想气体．P0和T0分别为大气的压强和温度．已知：气体内能U与温度T的关系为U=αT，α为正的常量；容器内气体的所有变化过程都是缓慢的．求
(1)气缸内气体与大气达到平衡时的体积V1；
(2)在活塞下降过程中，气缸内气体放出的热量Q。