如图,两个长均为L的轻质杆,通过A、B、C上垂直纸面的转动轴与A、B、C三个物块相连,整体处于竖直面内。A、C为两个完全相同的小物块,B物块的质量与A小物块的质量之比为2∶1,三个物块的大小都可忽略不计。A、C两物块分别带有+q、-q的电荷量,并置于绝缘水平面上,在水平面上方有水平向右的匀强电场,场强为E,物块间的库仑力不计。当AB、BC与水平面间的夹角均为53°时,整体恰好处于静止状态,一切摩擦均不计,并且在运动过程中无内能产生,重力加速度为g。(sin53°=0.8,cos53°=0.6)
(1)求B物块的质量;
(2)在B物块略向下移动一些,并由静止释放后,它能否到达水平面?如果能,请求出B物块到达地面前瞬时速度的大小;如果不能,请求出B物块所能到达的最低位置。
运动员驾驶摩托车做腾跃特技表演是一种刺激性很强的运动项目。如图所示,AB是水平路面,BC是半径为20m的圆弧,CDE是一段曲面。运动员驾驶功率始终是P=1.8kW的摩托车在AB段加速,到B点时速度达到最大vm=20m/s,再经t=13s的时间通过坡面到达E点时,关闭发动机后水平飞出。已知人和车的总质量m=180 kg,坡顶高度h=5m,落地点与E点的水平距离s=16m,重力加速度g=10m/s2。如果在AB段摩托车所受的阻力恒定,求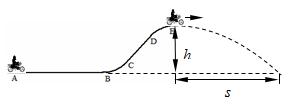
AB段摩托车所受阻力的大小;
摩托车过B点时受到地面支持力的大小;
摩托车在冲上坡顶的过程中克服阻力做功。
如下图所示,甲图是用来使带正电的离子加速和偏转的装置。乙为该装置中加速与偏转电场的等效模拟图。以y轴为界,左侧为沿x轴正向的匀强电场,场强为E。右侧为沿y轴负方向的另一匀强电场。已知OA⊥AB,OA=AB,且OB间的电势差为U0。若在x轴的C点无初速地释放一个电荷量为q、质量为m的正离子(不计重力),结果正离子刚好通过B点,求: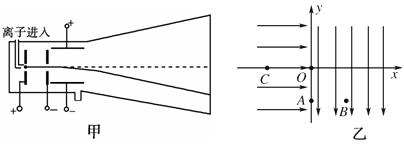
CO间的距离d;
粒子通过B点的速度大小。
2011年3月11日,日本大地震以及随后的海啸给日本带来了巨大的损失。灾后某中学的部分学生组成了一个课题小组,对海啸的威力进行了模拟研究,他们设计了如下的模型:如图甲在水平地面上放置一个质量为m=4kg的物体,让其在随位移均匀减小的水平推力作用下运动,推力F随位移x变化的图像如图乙所示,已知物体与地面之间的动摩擦因数为μ=0.5,g=10m/s2。
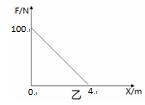
运动过程中物体的最大加速度为多少?
在距出发点什么位置时物体的速度达到最大?
物体在水平面上运动的最大位移是多少?
滑雪运动中当滑雪板压在雪地时会把雪内的空气逼出来,在滑雪板与雪地间形成一个暂时的“气垫”,从而大大减小雪地对滑雪板的摩擦。然而当滑雪板相对雪地速度较小时,与雪地接触时间超过某一值就会陷下去,使得它们间的摩擦力增大。假设滑雪者的速度超过4m/s时,滑雪板与雪地间的动摩擦因数就会由μ1=0.25变为μ2=0.125。一滑雪者从倾角θ=37°的坡顶A处由静止开始自由下滑,滑至坡底B(B处为一光滑小圆弧)后又滑上一段水平雪地,最后停在C处,如图所示,不计空气阻力,坡长L=26m,取g=10m/s2,sin37°=0.6,cos37°=0.8,求: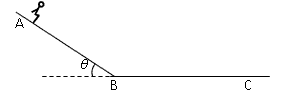
(1)滑雪者从静止开始到动摩擦因数发生变化所经历的时间;
(2)滑雪者到达B处的速度;
(3)滑雪者在水平雪地上运动的最大距离。
如图所示,一质量为m的滑块以 的速度从水平直轨道上的a点滑行距离S=1.0m后开始沿竖直平面的半圆形光滑轨道运动,滑块与水平直轨道间的动摩擦因数为μ=" 0.45" ,水平直轨道与半圆形轨道相切连接,半圆形轨道半径为R,滑块到达半圆形轨道最高点b时恰好不受压力.试求:
的速度从水平直轨道上的a点滑行距离S=1.0m后开始沿竖直平面的半圆形光滑轨道运动,滑块与水平直轨道间的动摩擦因数为μ=" 0.45" ,水平直轨道与半圆形轨道相切连接,半圆形轨道半径为R,滑块到达半圆形轨道最高点b时恰好不受压力.试求: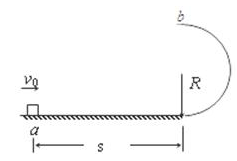
(1)滑块刚进入半圆形轨道时的速度和圆形轨道的半径R
(2)滑块落回到水平直轨道时离a点的距离
(3)如果仅给滑块在水平直轨道上运动的过程中施加一个水平方向恒定外力F,当外力F满足什么条件时,滑块离开最高点b后正好落回a点