有一种测量压力的电子秤,其原理图如图所示。E是内阻不计、电动势为6V的电源。R0是一个阻值为400Ω的限流电阻。G是由理想电流表改装成的指针式测力显示器。R是一个压敏电阻,其阻值可随压力大小变化而改变,其关系如下表所示。C是一个用来保护显示器的电容器。秤台的重力忽略不计。试分析:
| 压力F/N |
0 |
50 |
100 |
150 |
200 |
250 |
300 |
| 电阻R/Ω |
300 |
280 |
260 |
240 |
220 |
200 |
180 |
(1)利用表中的数据归纳出电阻R随压力F变化的函数式
(2)若电容器的耐压值为5V,该电子秤的最大称量值为多少牛顿?
(3)通过寻求压力与电流表中电流的关系,说明该测力显示器的刻度是否均匀?
在竖直的井底,将一物块以11 m/s的速度竖直的向上抛出,物体冲过井口时被人接住,在被人接住前1s内物体的位移是4 m,位移方向向上,不计空气阻力,g取10 m/s2,求:
(1)物体从抛出到被人接住所经历的时间;
(2)此竖直井的深度.
如下图所示,A、B两物体叠放在水平地面上,已知A、B的质量分别为 mA=10 kg, mB=20 kg,A、B之间,B与地面之间的动摩擦因数均为μ=0.5.一轻绳一端系住物体A,另一端系于墙上,绳与竖直方向的夹角为37°,今欲用外力将物体B匀速向右拉出,求所加水平力F的大小,并画出A、B的受力分析图.(取g=10 m/s2,sin 37°=0.6,cos 37°=0.8)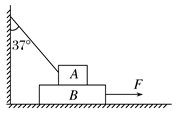
如右图所示,匀强电场E=4V/m,方向水平向左,匀强磁场 B=2T,方向垂直纸面向里。m=1g带正电的小物块A,从M点沿绝缘粗糙的竖直壁无初速下滑,它滑行0.8m到N点时就离开壁做曲线运动,在P点A瞬时受力平衡,此时其速度与水平方向成45°角。设P与M的高度差为1.6m。(g取10m/s2) 求: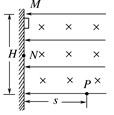
(1)A沿壁下滑时摩擦力做的功;
(2)P与M的水平距离。
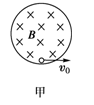
在竖直平面内有一圆形绝缘轨道,半径为R=0.4m,匀强磁场垂直于轨道平面向里,一质量为m=1×10-3kg、带电量为q=+3×10-2C的小球,可在内壁滑动,如图甲所示,开始时,在最低点处给小球一个初速度v0,使小球在竖直平面内逆时针做圆周运动,如图乙(a)是小球在竖直平面内做圆周运动的速率v随时间变化的情况,图乙(b)是小球所受轨道的弹力F随时间变化的情况,结合图象所给数据,(取g=10m/s2) 求:
(1)磁感应强度的大小;
(2)初速度v0的大小。
如右图所示的电路中,电源电动势E=6.0V,内阻r=0.6Ω,电阻R2=0.5Ω,当开关S断开时;电流表的示数为1.5A,电压表的示数为3.0V,试求:
(1)电阻R1和R3的阻值;
(2)当S闭合后,电压表的示数、以及R2上消耗的电功率。