美国物理学家密立根用精湛的技术测量光电效应中几个重要的物理量,这项工作成了爱因斯坦方程式在很小误差范围内的直接实验证据.密立根的实验目的是:测量金属的遏止电压Uc.与入射光频率ν,由此计算普朗克常量h,并与普朗克根据黑体辐射得出的h相比较,以检验爱因斯坦光电效应方程式的正确性.如图所示是根据某次实验作出的Uc-ν图象,电子的电荷量为1.6×10-19C.试根据图象求:这种金属的截止频率νc和普朗克常量h.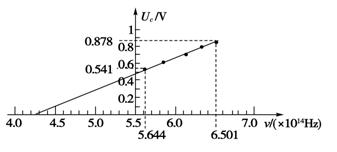
如图所示,电源电动势E="2" V,r="0.5" Ω,竖直导轨宽L="0.2" m,导轨电阻不计,另有一金属棒质量m="0.1" kg、电阻R="0.5" Ω,它与导轨间的动摩擦因数μ=0.4,靠在导轨的外面.为使金属棒静止不滑动,施一与纸面夹角为30°且与导体棒垂直指向纸里的匀强磁场,g取10 m/s2,求: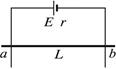
(1)此磁场的方向;
(2)磁感强度B的取值范围.
如图所示,一个半径R=1.0m的圆弧形光滑轨道固定在竖直平面内,轨道的一个端点B和圆心O的连线与竖直方向夹角θ=60°,C为轨道最低点,D为轨道最高点.一个质量m=0.50kg的小球(视为质点)从空中A点以v0=4.0m/s的速度水平抛出,恰好从轨道的B端沿切线方向进入轨道.重力加速度g取10m/s2.试求:
(1)小球抛出点A距圆弧轨道B端的高度h.
(2)小球经过轨道最低点C时对轨道的压力FC.
(3)小球能否到达轨道最高点D?若能到达,试求对D点的压力FD.若不能到达,试说明理由.
2007年10月24日18时05分,中国第一颗探月卫星“嫦娥一号”在西昌卫星发射中心成功升空,“嫦娥奔月”成为中国航天的现实. 为了方便研究,我们将“嫦娥奔月”的过程简化为:“嫦娥一号”升空后,首先进入周期为T1的近地圆轨道,然后在地面的指令下经过一系列的变轨后最终被月球捕获,在距离月球表面为h的轨道上绕月球做匀速圆周运动. 已知地球质量为M1,半径为R1,月球质量为M2,半径为R2。求:“嫦娥一号”绕月球运动时的周期T2(最终结果用题目中的物理量来表示).
滑板运动是一项非常刺激的水上运动,研究表明,在进行滑板运动时,水对滑板的作用力Fx垂直于板面,大小为kv2,其中v为滑板速率(水可视为静止)。某次运动中,在水平牵引力作用下,当滑板和水面的夹角θ=37°时,滑板做匀速直线运动,相应的k="54" kg/m,人和滑板的总质量为108 kg,试求(重力加速度g取10 m/s2,sin 37°=0.6,忽略空气阻力):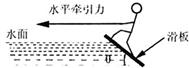
(1)水平牵引力的大小;
(2)滑板的速率;
如图,质量为m的b球用长h的细绳悬挂于水平轨道BC的出口C处。质量也为m的小球a,从距BC高h的A处由静止释放,沿ABC光滑轨道滑下,在C处与b球正碰并与b粘在一起。已知BC轨道距地面有一定的高度,悬挂b球的细绳能承受的最大拉力为2.8mg。试问:
①a与b球碰前瞬间的速度多大?
②a、b两球碰后,细绳是否会断裂?(要求通过计算回答)