如图所示在粗糙的水平面有一个长盒A，盒的内部完全光滑，盒子长度为L，盒与水平面间的动摩擦因数μ=3/4，盒紧靠左侧有一物块B，A与B均处在某一特定场区中，场区对A、B均始终有向右的恒定作用力F=mg/2，已知盒子质量与物块的质量均为m。现同时释放A、B，此后B与A每次碰撞都是完全弹性碰撞（即每次碰撞均交换速度，且碰撞时间极短，可以忽略不计）。已知重力加速度为g。求：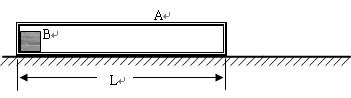
（1）物块B从开始释放到与盒A发生第一次碰撞所经过的时间t1．
（2）B与A发生第一次碰撞后，A运动的加速度大小aA和发生第二次碰撞前瞬间物块B的速度大小v2．
（3）盒A在水平面上运动的总位移大小x．
(15分)轻弹簧秤上端固定于O点，下端悬挂一个光滑的定滑轮C，已知C重1N，木块A、B用跨过定滑轮的轻绳连接，A、B的重力分别为5N和2N。整个系统处于平衡状态，如图所示，求：
(1)地面对木块A的支持力大小；
(2)弹簧秤的示数，
(3)滑轮C受到的合力。
．如图所示，质量m＝5.0X10-8千克的带电粒子，以初速Vo=2m/s的速度从水平放置的平行金属板A、B的中央，水平飞入电场，已知金属板长0.1m，板间距离d＝2X10-2m，当UAB=1000V时，带电粒子恰好沿直线穿过电场，若两极板间的电势差可调，要使粒子能从两板间飞出，UAB的变化范围是多少?(g取10m／s2)
如图所示，炽热金属丝上发射的电子(假设刚离开金属丝时的速度为0)，经电压U1＝4500 V加速后，以v0的速度垂直进入偏转电场，并能从偏转电场离开．偏转电场两极板间的电压U2＝180 V，距离d＝2 cm，板长L＝8 cm.电子的质量m＝0.9×10－30 kg，电子的电荷量e＝1.6×10－19 C．求：
(1)v0的大小；
(2)电子在离开偏转电场时的纵向偏移量．
如图所示，一个质量m＝30 g，带电量q＝－1.5×10－8 C的半径极小的小球，用绝缘丝线悬挂在水平方向的匀强电场中．当小球静止时，测得悬线与竖直方向成45°夹角．求：
(1)小球受到的电场力的大小和方向；
(2)该电场的电场强度的大小和方向．
(12分)在光滑水平面上固定一个内壁光滑的竖直圆环S（右图为俯视图），圆环半径为R="lm." 一根长r=0.5m的绝缘细线一端固定于圆环圆心D点，另一端系住一个质量为m=0.2kg、带电量为q=+5×10 - 5C的小球．空间有一场强为E=4xl04N/C的匀强电场，电场方向与水平面平行．将细线拉至与电场线平行，给小球大小为10m/s、方向垂直于电场线的初速度vo．
(1)求当小球转过90°时的速度大小；
(2)若当小球转过90°时，细线突然断裂，小球继续运动，碰到圆环后不反弹，碰撞后，小球垂直于碰撞切面方向的速度因能量损失减小为零，平行于碰撞切面方向的速度大小保持不变．之后小球沿圆环内壁继续做圆周运动．求这一运动过程中的速度的最小值．
(3)从初始位置开始，要使小球在运动过程中，细线始终保持不松弛，求电场强度E的大小所需满足的条件．