已知抛物线 的焦点
的焦点 与椭圆
与椭圆 的一个焦点重合,它们在第一象限内的交点为
的一个焦点重合,它们在第一象限内的交点为 ,且
,且 与
与 轴垂直,则椭圆的离心率为( )
轴垂直,则椭圆的离心率为( )
A. |
B. |
C.  |
D. |
已知随机事件A与B,经计算得到 的范围是3.841<
的范围是3.841< <6.635,则(下表是
<6.635,则(下表是 的临界值表,供参考)
的临界值表,供参考)
P( ≥x0) ≥x0) |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| x0 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
A. 有95% 把握说事件A与B有关 B. 有95% 把握说事件A与B无关
C. 有99% 把握说事件A与B有关 D. 有99% 把握说事件A与B无关
已知命题 ,
, ,则
,则 为
为
A.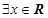 , , |
B. , , |
C. , , |
D. , , |
设 ,则
,则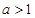 是
是 的
的
| A.充分但不必要条件 | B.必要但不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
如图,某人向圆内投镖,如果他每次都投入圆内,那么他投中正方形区域的概率为
A. |
B.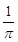 |
C. |
D. |
某品牌产品,在男士中有10%使用过,女士中有40%的人使用过,若从男女人数相等的人群中任取一人,恰好使用过该产品,则此人是位女士的概率是
A.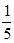 |
B. |
C. |
D.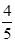 |