如图所示:轻弹簧一端连于固定点O，可在竖直平面内自由转动；另一端连接一带电小球P，其质量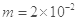
kg，电荷量q=0.2C。将弹簧保持原长拉至水平后，以初速度
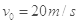竖直向下射出小球P，小球P到达O点的正下方
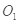点时速度恰好水平，其大小v=15m/s。若
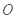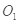、相距R=1.5m，小球P在点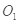与另一由细绳悬挂的、不带电的、质量
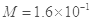kg的静止绝缘小球N相碰。碰后瞬间，小球P脱离弹簧，小球N脱离细绳，同时在空间加上竖直向上的匀强电场E和垂直于纸面的磁感应强度B=lT的匀强磁场。此后，小球P在竖直平面内做半径r=0.5m的匀速圆周运动。小球P、N均可视为质点，小球P的电荷量保持不变，不计空气阻力，取
。则。
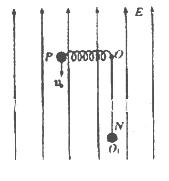
(1)判断小球P所带电性，并说明理由。
(2)弹簧从水平摆至竖直位置的过程中，其弹性势能变化了多少？
(3)请通过计算并比较相关物理量，判断小球P、N碰撞后能否在某一时刻具有相同的速度。
(8分)如图所示，重力G1＝8 N的砝码悬挂在绳PA和PB的结点上， PA偏离竖直方向37°角，PB水平且连在所受重力为G2＝100 N的木块上，木块静止于倾角为37°的斜面上， (取
，已知
，
)，试求：
(1) 绳PB上的拉力的大小
(2)木块所受斜面的弹力与摩擦力.
(10分)在一条平直公路上，甲、乙两辆汽车原来静止，乙车在前，甲车在后，两者之间的距离为l0=85m，t=0时甲车开始向右做匀加速直线运动，加速度a1=2.5m/s2，甲车运动t0=6.0s后，乙车开始向右做匀加速直线运动，加速度a2=5.0m/s2，求：
(1)乙车开始运动时两车之间的距离
(2)经多长时间两车第一次相遇
(3)两次相遇之间两车的最远距离
(7分)从160 m高空静止的汽球上自由落下一物体，此物体下落第2 s末张开降落伞匀速下落，求物体落到地面上所用的时间。
(8分)如图所示，在矩形abcd区域内存在着匀强磁场，两个不同带电粒子从顶角c处沿cd方向射入磁场，分别从p、q两处射出。已知cp连线和cq连线与ca边分别成30°和60°角，不计两粒子的重力。
（1）若两粒子的比荷相同，求两粒子在磁场中运动的时间之比；
（2）若两粒子比荷不同，但都是由静止经同一电场加速后进入磁场的，求两粒子在磁场中运动的速率之比。
(12分)如图所示，在直角坐标系的第二象限和第四象限中的直角三角形区域内，分布着磁感应强度均为B=5.0×10-3T的匀强磁场，方向分别垂直纸面向外和向里。一质量m=6.4×10-27kg、电荷量q=+3.2×10-19C的带电粒子（带电粒子重力不计），由静止开始经加速电压U=1250V的电场（图中未画出）加速后，从坐标点M（-4,
）m处平行于x轴向右运动，并先后通过两个匀强磁场区域。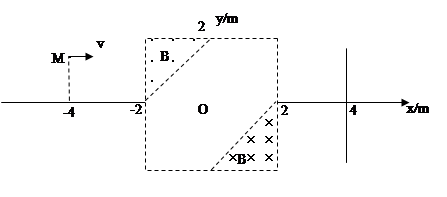
（1）求带电粒子在磁场中的运动半径；（结果保留根号）
（2）在图中画出从直线x=-4m到直线x=4m之间带电粒子的运动轨迹；
（3）求出带电粒子在两个磁场区域偏转所用的时间。