如图所示，在竖直平面内，粗糙的斜面轨道AB的下端与光滑的圆弧轨道BCD相切于B点，C点是最低点，圆心角∠BOC＝37°，D点与圆心O点等高，圆弧轨道半径R＝1.0 m，现在一个质量为m＝0.2 kg可视为质点的小物体，从D点的正上方E点处自由下落，DE距离h＝1.6 m，小物体与斜面AB之间的动摩擦因数μ＝0.5.取sin37°＝0.6，cos37°＝0.8，g＝10 m/s2。求：
(1)小物体第一次通过C点时轨道对小物体的支持力N的大小；
(2)要使小物体不从斜面顶端飞出，斜面的长度LAB至少要多长；
(3)若斜面已经满足(2)要求，小物体从E点开始下落，直至最后在光滑圆弧轨道做周期性运动，在此过程中系统因摩擦所产生的热量Q的大小．
(9分)如图所示，玻璃管粗细均匀（粗细可忽略不计），竖直管两封闭端内理想气体长分别为上端30cm、下端27cm，中间水银柱长10cm。在竖直管如图位置接一水平玻璃管，右端开口与大气相通，用光滑活塞封闭5cm长水银柱。大气压p0＝75cmHg。
①求活塞上不施加外力时两封闭气体的压强各为多少？
②现用外力缓慢推活塞恰好将水平管中水银全部推入竖直管中，求这时上下两部分气体的长度各为多少？
如图所示，在第一、二象限存在场强均为E的匀强电场，其中第一象限的匀强电场的方向沿x轴正方向，第二象限的电场方向沿x轴负方向。在第三、四象限矩形区域ABCD内存在垂直于纸面向外的匀强磁场，矩形区域的AB边与x轴重合。M点是第一象限中无限靠近y轴的一点，在M点有一质量为m、电荷量为e的质子，以初速度v0沿y轴负方向开始运动，恰好从N点进入磁场，若OM＝2ON，不计质子的重力，试求：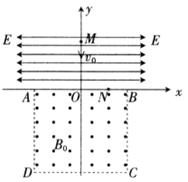
（1）N点横坐标d；
（2）若质子经过磁场最后能无限靠近M点，则矩形区域的最小面积是多少；
（3）在（2）的前提下，该质子由M点出发返回到无限靠近M点所需的时间。
某中学的部分学生组成了一个课题小组，对海啸的威力进行了模拟研究，他们设计了如下的模型：如图甲在水平地面上放置一个质量为m=4kg的物体，让其在随位移均匀减小的水平推力作用下运动，推力F随位移x变化的图像如图乙所示，已知物体与地面之间的动摩擦因数为μ=0.5，g=10m/s2，则：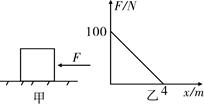
（1）运动过程中物体的最大加速度为多少？
（2）在距出发点什么位置时物体的速度达到最大？
（3）物体在水平面上运动的最大位移是多少？
如图所示，直角玻璃三棱镜ABC置于空气中，棱镜的折射率为n=
，∠A= 60°。一细光束从AC的中点D垂直AC面入射，AD =a，求：
①光从棱镜第一次射入空气时的折射角。
②光从进入棱镜到它第一次从棱镜中射出所经历的时间（光在真空中的传播速度为c）。
桌面上有一玻璃圆锥，圆锥的轴（图中虚线）与桌面垂直，过轴线的截面为等边三角形，此三角形的边长为L，如图所示，有一半径为
的圆柱形平行光束垂直底面入射到圆锥上，光束的中心轴与圆锥的轴重合。已知玻璃的折射率为
，求：
①光在玻璃中的传播速度是多少？
②光束在桌面上形成的光斑的面积是多少？