为了使粒子经过一系列的运动后,又以原来的速率沿相反方向回到原位,可设计如下的一个电磁场区域(如图所示):水平线QC以下是水平向左的匀强电场,区域Ⅰ(梯形PQCD)内有垂直纸面向里的匀强磁场,磁感应强度为B;区域Ⅱ(三角形APD)内的磁场方向与Ⅰ内相同,但是大小可以不同,区域Ⅲ(虚线PD之上、三角形APD以外)的磁场与Ⅱ内大小相等、方向相反.已知等边三角形AQC的边长为2l,P、D分别为AQ、AC的中点.带正电的粒子从Q点正下方、距离Q点为l的O点以某一速度射出,在电场力作用下从QC边中点N以速度v0垂直QC射入区域Ⅰ,再从P点垂直AQ射入区域Ⅲ,又经历一系列运动后返回O点.(粒子重力忽略不计)求: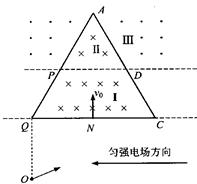
(1)该粒子的比荷.
(2)粒子从O点出发再回到O点的整个运动过程所需时间.
质量m=0.2kg的物体从高H=20m的楼顶由静止开始下落,经过时间t=2.5s后着地,(g=10m/s2),求:
(1) 物体受到的空气阻力的大小
(2)重力对物体做的功和空气阻力对物体做的功
(3)合外力对物体做的功
(4)刚要着地时重力的瞬时功率
如图所示,质量m=1 kg的小球用细线拴住,线长l=0.5 m,细线所受拉力达到F=18 N时就会被拉断。当小球从图示位置释放后摆到悬点的正下方时,细线恰好被拉断。若此时小球距水平地面的高度h=5 m,重力加速度g=10 m/s2,求小球落地处到地面上P点的距离?(P点在悬点的正下方)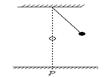
水平抛出的一个石子,经过0.4s落到地面,落地时的速度方向跟水平方向的夹角是53° ,(g取10m/s2)。试求:(1)石子的抛出点距地面的高度;(2)石子抛出的水平初速度。(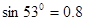
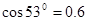 )
)
图为一理想变压器,ab为原线圈,ce为副线圈,d为副线圈引出的一个接头。原线圈入正弦式交变电压的u-t图象如题13-2图所示。若只在ce间接一只Rce="400" Ω的电阻,或只在de间接一只Rde="225" Ω的电阻,两种情况下电阻消耗的功率均为80W。
(1)请写出原线圈输入电压瞬时值Uab的表达式;
(2)求只在ce间接400Ω的电阻时,原线圈中的电流I1;
(3)求ce和de 间线圈的匝数比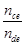 。
。
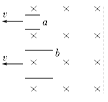
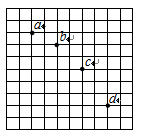
如右图所示,用粗细相同的铜丝做成边长分别为L和2L的两只闭合线框a和b,以相同的速度从磁感应强度为B的匀强磁场区域中匀速地拉到磁场外,不考虑线框的动能,若外力对环做的功分别为Wa、Wb,则Wa∶Wb为多少?