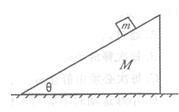
在光滑水平面上，有一个粗细均匀的单匝正方形线圈abcd，现在外力的作用下从静止开始向右运动，穿过固定不动的有界匀强磁场区域，磁场的磁感应强度为B，磁场区域的宽度大于线圈边长。测得线圈中产生的感应电动势ε的大小和运动时间变化关系如图。已知图像中三段时间分别为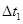
、
、
，且在时间内外力为恒力。
（1）定性说明线圈在磁场中向右作何种运动？
（2）若线圈bc边刚进入磁场时测得线圈速度
，bc两点间电压U，求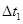时间内，线圈中的平均感应电动势。
（3）若已知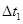∶∶=2∶2∶1，则线框边长与磁场宽度比值为多少？
（4）若仅给线圈一个初速度v0使线圈自由向右滑入磁场，试画出线圈自bc边进入磁场开始，其后可能出现的
图像。（只需要定性表现出速度的变化，除了初速度
外，不需要标出关键点的坐标）
亚运会男篮决赛过程中，王治郅为了避免韩国的抢断，弹地传球（篮球比赛运动员为了避免对方运动员对篮球的拦截，往往采取使篮球与地面发生一次碰撞反弹而传递给队友的传球方法）给队员刘炜。假设王治郅将篮球以v0=5m/s的速率从离地面高h=0.8m处水平抛出，球与地面碰后水平方向的速度变为与地面碰前瞬间水平速度的4/5，球与地面碰后竖直方向的速度变为与地面碰前瞬间竖直方向速度的3/4
，刘炜恰好在篮球的速度变为水平时接住篮球，篮球与地面碰撞作用的时间极短（可忽略不计），不计空气阻力，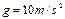
，求王治郅、刘炜传球所用的时间和王治郅抛球位置与刘炜接球位置之间的水平距离分别是多少？
如图所示，固定的半圆弧形光滑轨道置于水平方向的勻强电场和匀强磁场中，轨道圆弧半径为R，磁感应强度为B，方向垂直于纸面向外，电场强度为£；，方向水平向左.一个质量为m的小球(可视为质点)放在轨道上的C点恰好处于静止，圆弧半径OC与水平直径AD的夹角为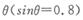
。
(1)求小球带何种电荷，电荷量是多少？并说明理由。
(2)如果将小球从A点由静止释放，小球在圆弧轨道上运动时，对轨道的最大压力的大小是多少？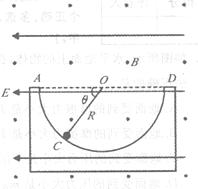
实验室需要用电子打击静止在P点的粒子,先让电子在直线加速器中经过电压U加速，再从小孔O沿
’方向水平飞出。已知OP的距离为d，OP与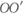
的夹角为θ，电子的质量为m，电量为-e，要想电子能打到P点，可在直线加速器左侧加一个垂直于纸面的磁场，求磁感应强度的表达式并说明方向。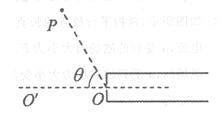
质量为500吨的机车以恒定的功率由静止出发，经5min行驶2. 25km,速度达到最大值54km/h，设阻力恒定。问：（1)机车的功率P多大？（2)机车的速度为36 km/h时机车的加速度a多大？
如图所示，质量M、倾角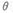
为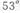
的木楔静止于粗糙水平地面上，有一质量m =10Kg的物块由静止开始沿木楔斜面下滑，当下滑位移X=1Om时，其速度v=10m/s 在这个过程中木楔处于静止状态。求:木块与木楔间的动摩擦因数(取
="0.8" g=1Om/s2