如图甲所示，竖直平面内的光滑轨道由倾斜直轨道AB和圆轨道BCD组成，AB和BCD相切于B点，CD连线是圆轨道竖直方向的直径（C、D为圆轨道的最低点和最高点），已知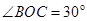
。可视为质点的小滑块从轨道AB上高H处的某点由静止滑下，用力传感器测出滑块经过圆轨道最高点D时对轨道的压力为F，并得到如图乙所示的压力F与高度H的关系图象，取
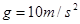。求：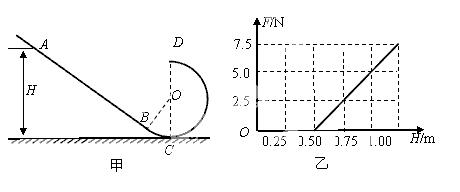
（1）滑块的质量和圆轨道的半径；
（2）是否存在某个H值，使得滑块经过最高点D后能直接落到直轨道AB上与圆心等高的点。若存在，请求出H值；若不存在，请说明理由。
如图2－7－21所示，在A、B两点间接一电动势为4 V，内阻为1 Ω的直流电源，电阻R1、R2、R3的阻值均为4 Ω，电容器的电容为30 μF，电流表的内阻不计，求：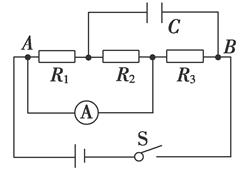
图2－7－21
(1)电流表的读数；
(2)电容器所带的电荷量；
(3)断开电源后，通过R2的电荷量．
如图2－8－21所示是把量程为3 mA的电流表改装成欧姆表的结构示意图，其中电池的电动势E＝1.5 V，经改装后，若将原电流表3 mA刻度处的刻度值定为零位置，则2 mA刻度处应标多少阻值？当用它测量某电阻时，指针恰好指在中间位置，被测电阻为多少？
图2－8－21
一个电解槽中，单位体积内的正负离子数都为n，每个离子的带电量为q，正负离子的平均定向速度率都为v，电解槽的横截面积为S，试求通过电解槽的电流强度。
来自质子源的质子（初速为0），经一加速电压为800kV的直线加速器加速，形成电流为1mA的细柱形质子流。已知质子的电量为e=1.6×10-19C，这束质子流每秒钟打到靶上的质子数是多少？假定分布在质子源到靶之间的加速电场是均匀的，质子束中与质子源相距L和4L的两处，各取一段极短的相等长度的质子流，其中质子数分别为n1和n2，求n1和n2的比值。
如图所示，ab是半径为R的圆的一条直径，该圆处于匀强电场中，电场强度大小为E，方向一定，在圆周所在的平面内将一个带正电q的小球从a点以相同的动能抛出，抛出方向不同时，小球会经过圆周上不同的点，在所有的点中，到达c点时小球的动能最大，已知∠cab=30º，若不计重力和空气阻力，则：
⑴电场方向与ac间的夹角θ多大？
⑵若小球在a点时初速度方向与电场方向垂直，且小球恰好能落在c点，则初动能多大？[θ=∠Oca=∠cab=30º；Ek=
]