宇航员站在某一星球表面上的某高处，沿水平方向抛出一小球。经过时间t，小球落到星球表面，测得抛出点与落地点之间的距离为L。若抛出时的初速度增大到2倍，则抛出点与落地点之间的距离为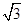
L。已知两落地点在同一水平面上，该星球的半径为R，万有引力常数为G。求该星球的质量M。
如图，在平面直角坐标系xoy内，第一象限的射线op与x轴夹角为30º，在∠pox范围之外存在垂直xoy面向里的匀强磁场，磁感应强度为B．一质量为m、带电量为q的正电粒子，从o点以沿y轴负方向的速度v出发仅受磁场力而运动。试求：
（1）粒子离开o点后，第三次经过磁场边界时的位置坐标；
（2）粒子在磁场中运动的总时间；
（3）若保持其它条件不变而将∠pox变为15º，粒子出发之后将总共几次穿越磁场边界？
在光滑的水平冰面上建立xOy平面直角坐标系：向东方向为x轴正方向，向南方向为y轴正方向。现有一质量为1kg的质点静止在坐标原点，从t = 0时刻开始，在第一个2s内对质点施加一个向东方向，大小为2N的水平拉力F；在第二个2s内将此力F改为向南方向，大小不变；第三个2s内再将此力F改为向东偏北45°方向，大小不变。求：
（1）第4s末质点的速度（结果可以用根式表达）；
（2）第6s末质点的位置坐标。
如图所示，半径为R的光滑圆环上套有一质量为m的小环，当圆环以角速度ω绕过环心的竖直轴旋转时，求小环稳定后偏离圆环最低点的高度h.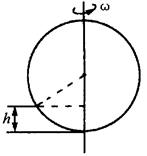
在勇气号火星探测器着陆的最后阶段，着陆器降落到火星表面上，再经过多次弹跳才停下来。假设着陆器第一次落到火星表面弹起后，到达最高点时高度为h，速度方向是水平的，速度大小为v0，求它第二次落到火星表面时速度的大小，计算时不计火星大气阻力。已知火星的一个卫星的圆轨道的半径为r，周期为T，火星可视为半径为r0的均匀球体。
土星周围有许多大小不等的岩石颗粒，其绕土星的运动可视为圆周运动。其中有两个岩石颗粒A和B与土星中心距离分别为rA＝8.0×104km和rB＝1.2×105km。忽略所有岩石颗粒间的相互作用。（结果可用根式表示）
（1）求岩石颗粒A和B的线速度之比；
（2）求岩石颗粒A和B的周期之比；
（3）土星探测器上有一物体，在地球上重为10 N，推算出他在距土星中心3.2×105km处受到土星的引力为0.38 N。已知地球半径为6.4×103km，请估算土星质量是地球质量的多少倍？