如图所示，一质量为m、电荷量为q、重力不计的微粒，从倾斜放置的平行电容器I的A板处由静止释放，A、B间电压为U1。微粒经加速后，从D板左边缘进入一水平放置的平行板电容器II，由C板右边缘且平行于极板方向射出，已知电容器II的板长为板间距离的2倍。电容器右侧竖直面MN与PQ之间的足够大空间中存在着水平向右的匀强磁场（图中未画出），MN与PQ之间的距离为L，磁感应强度大小为B。在微粒的运动路径上有一厚度不计的窄塑料板（垂直纸面方向的宽度很小），斜放在MN与PQ之间，
=45°。求：
（1）微粒从电容器I加速后的速度大小；
（2）电容器II CD间的电压；
（3）假设粒子与塑料板碰撞后，电量和速度大小不变、方向变化遵循光的反射定律，碰撞时间极短忽略不计，微粒在MN与PQ之间运动的时间和路程。
如图所示，靶盘竖直放置，A 、O两点等高且相距4m，将质量为20g的飞镖从A点沿AO方向抛出，经0.2s落在靶心正下方的B点．不计空气阻力，重力加速度取g=10m/s2．求：
（1）飞镖飞行中受到的合力；
（2）飞镖从A点抛出时的速度；
（3）飞镖落点B与靶心O的距离．
质量m=2kg的物体静止在水平面上，现在对物体施加一个大小F=10N的水平方向拉力，物体开始运动，2s末位移4m。（g取10m/s2）求：
（1）物体的加速度；
（2）滑动摩擦力大小；
（3）物体与水平面间的动摩擦因数µ。
一汽车在水平面上以72 km/h的初速度做匀减速直线运动，加速度大小为5 m/s2。求：
（1）汽车3 s时的速度；
（2）汽车从开始做匀减速直线运动到停止的位移。
物体只受两个力F1和F2的作用，其中F1＝30 N，方向水平向右；F2＝40 N，方向竖直向下。求解这两个力的合力F的大小和方向。
如图所示，区域Ⅰ、Ⅱ分别存在着有界匀强电场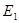
、
，已知区域Ⅰ宽
，区域II宽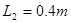
，
且方向与水平成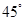
角斜向右上方，
且方向竖直向下。 电量为
质量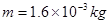
的带电小球 （可视为质点）由静止释放。（ 
）求：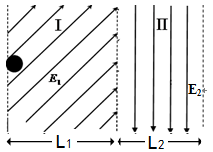
（1）小球在电场区域I中运动的加速度大小和时间
（2）小球离开电场区域II的速度大小和方向