已知函数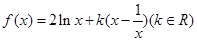 。
。
(1)当 时,求函数
时,求函数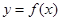 的单调区间;
的单调区间;
(2)求证:当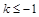 时,对所有的
时,对所有的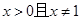 都有
都有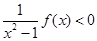 成立.
成立.
已知函数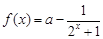 ,
,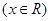 .
.
(1)用定义证明:不论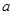 为何实数
为何实数 在
在 上为增函数;
上为增函数;
(2)若 为奇函数,求
为奇函数,求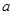 的值;
的值;
(3)在(2)的条件下,求 在区间[1,5]上的最小值.
在区间[1,5]上的最小值.
已知函数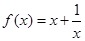 .
.
(1)判断函数的奇偶性,并加以证明;
(2)用定义证明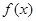 在
在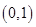 上是减函数;
上是减函数;
(3)函数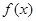 在
在 上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
某省两相近重要城市之间人员交流频繁,为了缓解交通压力,特修一条专用铁路,用一列火车作为交通车,已知该车每次拖4节车厢,一日能来回16次, 如果每次拖7节车厢,则每日能来回10次.
(1)若每日来回的次数是车头每次拖挂车厢节数的一次函数,求此一次函数解析式:
(2)在(1)的条件下,每节车厢能载乘客110人.问这列火车每天来回多少次才能使运营人数最多?并求出每天最多运营人数。
已知函数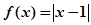 .
.
(1)用分段函数的形式表示该函数;
(2)在右边所给的坐标系中画出该函数的图象;
(3)写出该函数的定义域、值域、奇偶性、单调区间(不要求证明). 
设全集为实数集R,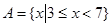 ,
,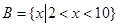 ,
, .
.
(1)求 及
及 ;
;
(2)如果 ,求a的取值范围.
,求a的取值范围.