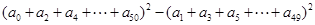统计表明：某种型号的汽车在匀速行驶中每小时的耗油量
（升）关于行驶速度
（千米/每小时）的函数解析式可以表示为
，已知甲、乙两地相距100千米.
（1）当汽车以40千米/小时的速度行驶时，从甲地到乙地要耗油多少升？
（2）当汽车以多大速度行驶时，从甲地到乙地耗油最少？最少为多少升？
求函数
的单调递增区间.
(10分)设
和
分别是先后抛掷一枚骰子得到的点数，用随机变量
表示方程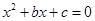
实根的个数（重根按一个计）．
（Ⅰ）求方程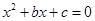有实根的概率；
（Ⅱ）求的分布列和数学期望；
（Ⅲ）求在先后两次出现的点数中有5的条件下，方程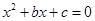有实根的概率.
(10分)某运动员射击一次所得环数
的分布如下：
|
0~6 |
7 |
8 |
9 |
10 |
 |
0 |
 |
 |
|
|
现进行两次射击，以该运动员两次射击中最高环数作为他的成绩，记为
.
(I)求该运动员两次都命中7环的概率
(II)求的分布列
(III)求的数学期望
(8分) 出租车司机从饭店到火车站途中有六个交通岗，假设他在各交通岗到红灯这一事件是相互独立的，并且概率都是
（I）求这位司机遇到红灯前，已经通过了两个交通岗的概率；
（II）求这位司机在途中遇到红灯数ξ的期望和方差。
(6分)已知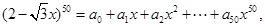
其中
是常数,计算