如图所示，电解槽A和电炉B并联接到电源上，电源内阻r＝1 Ω，电炉电阻R＝19 Ω，电解槽电阻r′＝0.5 Ω.当S1闭合、S2断开时，电炉消耗的功率为684 W；当S1、S2都闭合时，电炉消耗的功率为475 W．(电炉电阻不变)试求：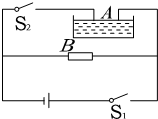
(1)电源电动势；
(2)S1、S2都闭合时，流过电解槽的电流大小；
(3)S1、S2都闭合时，电解槽消耗的电功率．
如图所示，一条轨道固定在竖直平面内，水平段ab粗糙，其距离为s=3m。在b点平滑过度，bcd段光滑，cd 段是以O为圆心、半径为R=0.4m的一小段圆弧。质量为m=2kg的小物块静止于a处，在一与水平方向成θ角的恒力F作用下 开始沿轨道匀加速运动，小物块到达b处时撤去该恒力，小物块继续运动到d处时速度水平，此时轨道对小物块的支持力大小为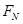
=15N。小物块与ab段的动摩擦因数为μ=0.5， g取10m/s2.求：
（1）小物块到达b点时的速度大小
；
（2）恒力F的最小值Fmin。（计算结果可以用分式或根号表示）
如图所示，一质量为1kg的小球套在一根固定的足够长光滑直杆上，直杆与水平面夹角θ为30°．现小球在F=15N的竖直向上的拉力作用下，从A点由静止出发向上运动．g 取10m/s2.试求：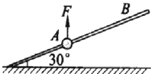
（1）小球运动的加速度a1；
（2）若F作用2s后撤去，小球上滑过程中距A点的最大距离sm
如图所示，宇航员站在某质量分布均匀的星球表面一斜坡上P点，沿水平方向以初速度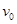
抛出一个小球，测得小球经时间t落到斜坡上另一点Q，斜面的倾角为α，已知该星球的半径为R．不考虑其它可能存在的阻力。求该星球上的第一宇宙速度
如图所示，一根长为L的绝缘轻绳的一端固定在O点，另一端连接着一个带正电的小球，小球可视为质点，其质量为m，电荷量为q。在O点正上方和正下方距O点L处，各固定一个绝缘弹性挡板A和B，两个挡板尺寸很小，均竖直放置。此装置处在一个竖直匀强电场中，电场强度的大小为
，方向最初竖直向上。现将小球拉到O点右侧同一高度且距O点L处，给它一个竖直向上的初速度V0=
。此后小球在A、B之间的右侧区域竖直面内做圆周运动，并不时与A、B挡板碰撞，在小球与A、B挡板碰撞时，通过两挡板上安装的传感器和控制电路，控制电场方向在碰后瞬间反向，不计碰撞中的能量损失，重力加速度为g，求：
（1）小球与A、B挡板第一次碰前瞬间，绳中的拉力分别为多少？
（2）若轻绳可以承受的最大拉力为50mg，则在绳断之前，小球与B挡板碰撞了多少次？
如图所示，电源的电动势E=110V，电阻R1=21Ω，电动机线圈的电阻R0=0.5Ω，当电键S断开时，电阻R1的电功率是525W，当S闭合时，电阻R1的电功率是336W，求：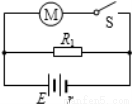
（1）电源的内阻；
（2）当S闭合时流过电源的电流和电动机消耗的功率。